秋田県高校入試「数学」大問4の解答・解説です。
入試の概要や他の問題を確認したい方は、下の記事をご覧ください。
なお、実際の入試問題や解答は、以下のサイトでご覧いただけます。

※問題や解説に登場する図やグラフは、すべて当サイトのデザイナーが作成したものです
大問4
(1)
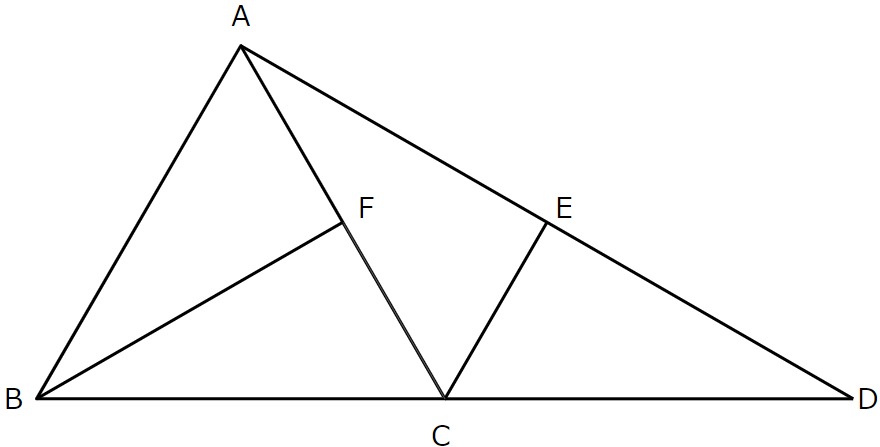
図のように,正三角形ABCがある。点Dは辺BCをCの方向に延長した直線上にある。点Eは線分AD上にあり,AB//ECである。点Fは辺AC上にあり,CE\(=\)CFである。このとき,△ACE\(\equiv\)△BCFとなることを証明しなさい。
答え&解き方
△ACEと△BCFにおいて
仮定から、CE\(=\)CF\(\cdots ①\)
正三角形は3つの辺が等しい三角形だから、AC\(=\)BC\(\cdots ②\)
平行線の錯角は等しいから、\(\angle\)ACE\(= \angle\)BAC
また、正三角形の3つの角は等しいから、\(\angle\)BAC\(= \angle\)BCF
よって、\(\angle\)ACE\(= \angle\)BCF\(\cdots ②\)
①、②、③より、2組の辺とその間の角がそれぞれ等しいから、
△ACE\(\equiv\)△BCF
ポイント
・三角形の合同条件を利用します
・正三角形の性質を使って、同じ長さの辺や同じ大きさの角を見つけます
(2)
詩織さんは,次のことがらの逆について考えたことをまとめた。[詩織さんのメモ]が正しくなるように,アには記述の続きを,イには反例を書きなさい。
2つの自然数 \(a, b\) において,\(a=3,b=6\) ならば,\(a+b=9\)
[詩織さんのメモ]
逆は,次のようにいえる。
2つの自然数 \(a,b\) において,
ア
逆は,正しくない。(反例)
イ
答え
ア:\(a+b=9\) ならば,\(a=3,b=6\)
イ:\(a=4,b=5\)
解き方
「○○ならば××」という命題があったとき、その逆は「××ならば○○」になります。
この問題では「2つの自然数 \(a,b\) において,\(a=3,b=6\) ならば,\(a+b=9\)」ということがらを考えているので、逆は「2つの自然数 \(a,b\) において,\(a+b=9\) ならば,\(a=3,b=6\) 」といえます。
次に逆への反例を考えていきましょう。
反例とは、あることがらが成り立たない例のことです。
今回は逆、つまり「2つの自然数 \(a,b\) において,\(a+b=9\) ならば,\(a=3,b=6\) 」が成り立たないことを証明する例を1つ挙げればよいわけです。
\(a+b=9\) になる \(a=3,b=6\) 以外の \(a,b\) の組み合わせを1つ答えれば正解です。
模範解答では \(a=2,b=7\) となっていますが、 \(a=1,b=8\) 、\(a=6,b=3\) なども正解です。
ポイント
・逆や反例といった言葉の意味を正確に理解しておく必要があります
(3)
直角三角形ABCで,辺ABの長さは,辺BCの長さより \(2 \ cm\) 長く,辺BCの長さは辺CAの長さより \(7 \ cm\) 長い。このとき,直角三角形ABCの斜辺の長さを求めなさい。
答え
\(17 \ cm\)
解き方
まずは、問題文からどの辺が一番長いのかを考えます。
辺ABは辺BCより \(2cm\) 長く、辺BCは辺CAより \(7cm\) 長いとあるので、最も長い辺は辺ABだと分かります。これが、三角形の斜辺にあたります。
ここで斜辺、すなわち辺ABの長さを \(x (cm)\) とすると、辺BCは \(x-2 (cm)\) 、辺CAは \((x-2)-7=x-9 (cm)\) と表すことができます。
これをまとめたのが下の図です。
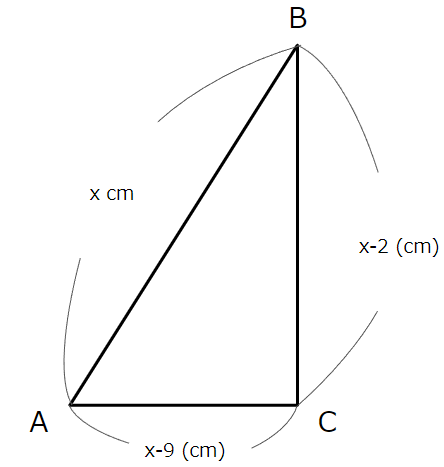
三平方の定理より、AB\(^{2}=\)BC\(^{2}+\)CA\(^{2}\) という方程式が成り立ちます。
ここに文字を代入して
\(\begin{eqnarray}
x^{2} &=& (x-2)^{2}+(x-9)^{2} \\[5pt]
x^{2} &=& (x^{2}-4x+4)+(x^{2}-18x+81) \\[5pt]
x^{2} &=& 2x^{2}-22x+85 \end{eqnarray}\)
右辺が0になるように式を整理して
\(\begin{eqnarray}
x^{2}-22x+85 &=& 0 \\[5pt]
(x-5)(x-17) &=& 0 \end{eqnarray}\)
\(x=5\) のとき、辺CAの長さが \(x-9=5-9=-4\) と負の数になってしまうため、不適。
よって、答えは \(x=17\) となり、求める斜辺の長さは \(17cm\) です。
ポイント
・求めたい長さを \(x\) と置いて、他の長さも文字を使って表してみます
・三平方の定理を用いて、辺の長さを求めます

