今回は前回の加法と減法に引き続き負の数が混ざった乗法（掛け算）と除法（割り算）について解説していきます。
―加法と減法について忘れてしまったひとはこちら（練習問題付き）
乗法
こちらも加法や減法のように「正の数と正の数」「正の数と負の数」「負の数と負の数」の組合せに分けて考えてみましょう。まず正の数と正の数の組合せについてですが、こちらは小学校で行っていた掛け算と変わりません。
次に正の数と負の数の組合せについてです。まず式と答えの例を見てみましょう。
\(1×(-2)=-2\)
このようになります。この負の数を含む乗法と除法においてつまづきやすい部分は符号についてだと思います。この負の数の持つーという符号は反対にすると意味と考えるとわかりやすいです。ここではコインなどを使って考えてみましょう。
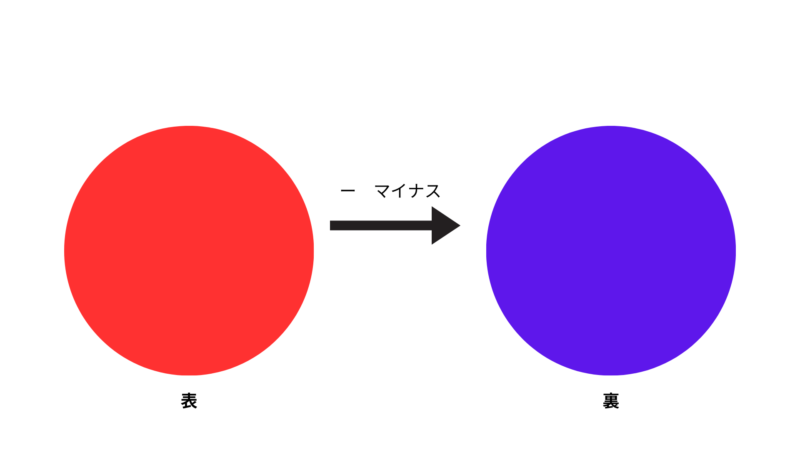
正の数は表（そのままにする）負の数は裏（コインを裏向きにする）と考えます。これを使って例の1×(-2)=-2という式の符号を考えてみましょう。まず、1は正の数なのでコインをそのままにします。次に負の数（-2）をかけているのでコインを裏返します。すると、コインは裏になります。よって答えの符号は負になります。そして数字の部分は小学校で習った掛け算と同じように計算するだけです。符号を考えずに計算すると1×2=2になります。これらの符号についてと数字についてをまとめると符号は負となり数字の部分は2なので、答えは-2となります。
次に負の数と負の数の組合せについて考えてみましょう。次はこの式を使って考えてみましょう。
\((-3)×(-2)=6\)
これを先ほどと同じように考えてみましょう。
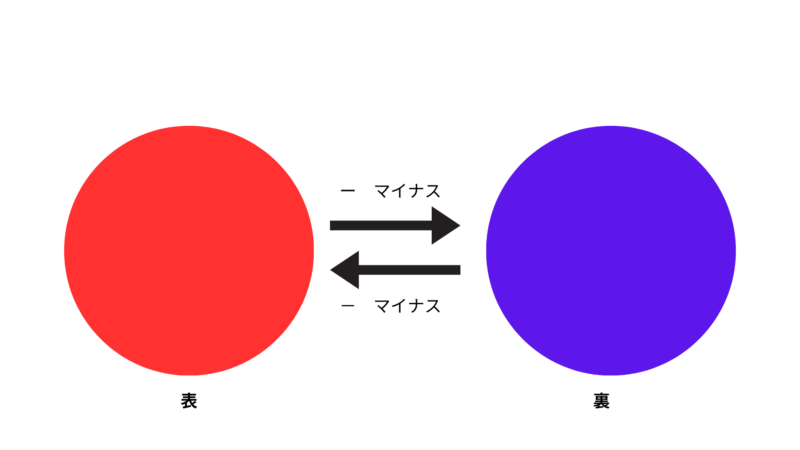
まず、（-3）は負の数なのでコインを裏返します。次に負の数（-2）をかけているのでコインを裏返します。すると、コインは表になります。よって答えの符号は正になります。そして数字の部分は符号を考えずに計算すると2×3=6よって答えは6です。
除法
除法も乗法と同じように3つの組合せに分けて計算します。乗法と同じように正の数と正の数では小学校の時の計算と同じです。
次に正の数と負の数の組合せを見てみましょう。
\(4÷(-2)=-2\)
例としてこの式を使います。先ほど乗法で行ったコインの考え方を同じように除法でも使うことができます。
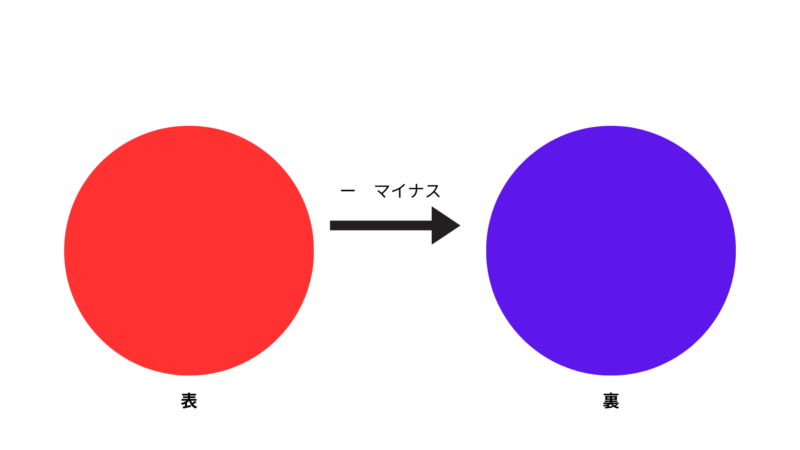
すると、符号は負となります。そして、数字は4÷2＝2となるので答えは-2になります。
最後に負の数と負の数の組合せについて考えてみましょう。
\((-9)÷(-3)=3\)
この式についても同じ方法で考えてみましょう。
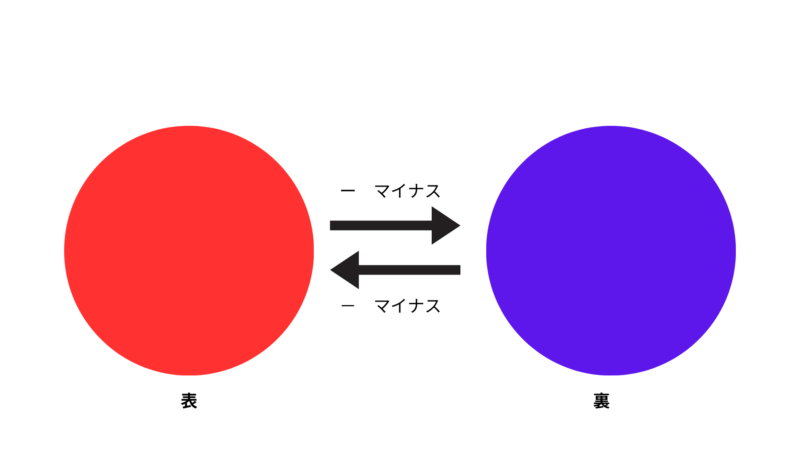
負の数と負の数よりコインは表となり、数字は3となるので答えは3です。
まとめ
このようにコインの裏表を考えると符号がわかりやすいです。そしてコインの裏の裏は表なので、負の数が2回でると表になることから、負の数が偶数回（0,2,4……)出てくるときの符号は正で奇数回(1,3,5……)ならば負ということがわかります。
「正の数と正の数」：正の数（正の数をいくつかけても正の数）
「正の数と負の数」：正の数or負の数（負の数が奇数回の場合は負の数、負の数が偶数回の場合は正の数）
「負の数と負の数」：正の数or負の数（負の数が奇数回の場合は負の数、負の数が偶数回の場合は正の数）
では、以下のように負の数が3つの場合はどのようにしてときますか？
\((-7)×(-10)×(-2)=-140\)
コインは裏→表→裏となりますね。今回の場合は、ー（マイナス）が奇数回あるので、答えは負の数になります。
