秋田県高校入試「数学」大問5の解答・解説です。
入試の概要や他の問題を確認したい方は、下の記事をご覧ください。
なお、実際の入試問題や解答は、以下のサイトでご覧いただけます。

※問題や解説に登場する図やグラフは、すべて当サイトのデザイナーが作成したものです
大問5
Ⅰ
次の図において,アは関数 \(y=x^2\),イは関数 \(y=ax^2 \ (0 \lt a \lt 1)\) のグラフである。2点 A,B は,アのグラフ上の点であり,点Aの座標は \((-1,1)\),点Bの座標は \((2,4)\) である。原点Oから \((0,1)\),\((1,0)\) までの距離を,それぞれ \(1cm\) とする。次の(1)~(3)の問いに答えなさい。【一部改題】
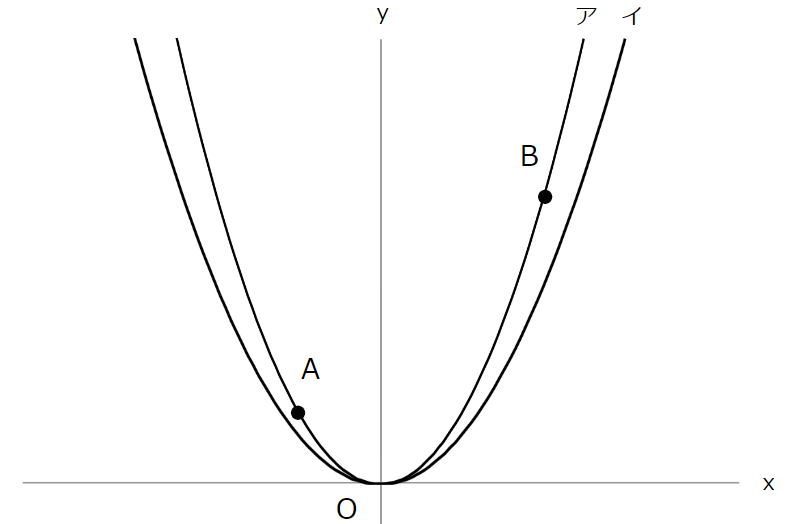
(1)
2点A,Bを通る直線の式を求めなさい。求める過程も書きなさい。
答え&解き方
求める直線は、2点A\((-1,1)\)、 B\((2,4)\)を通るので、傾きは、
\(\dfrac{4-1}{2-(-1)}=\dfrac{3}{3}=1\)
したがって、求める直線は \(y=x+b\) と表すことができます。
この直線はA\((-1,1)\)を通るから、先ほどの式に \(x=-1,y=1\) を代入すると、
\(1=-1+b\)
これを解くと、\(b=2\)
よって、求める直線の式は \(y=x+2\) になります。
ポイント
・2点の座標を使って、グラフの傾きを求めます
・傾きと切片が分かれば、一次関数の直線のグラフを求められます
(2)
\(a=\dfrac{2}{3}\) のとき,イのグラフ上に,\(x\) 座標が \(3\) である点Cをとる。このとき,線分BCの長さを求めなさい。【一部改題】
答え
\(\sqrt5 \ cm\)
解き方
まず、下の図のようにグラフに点Cを書き加えて、BとCを結びます。
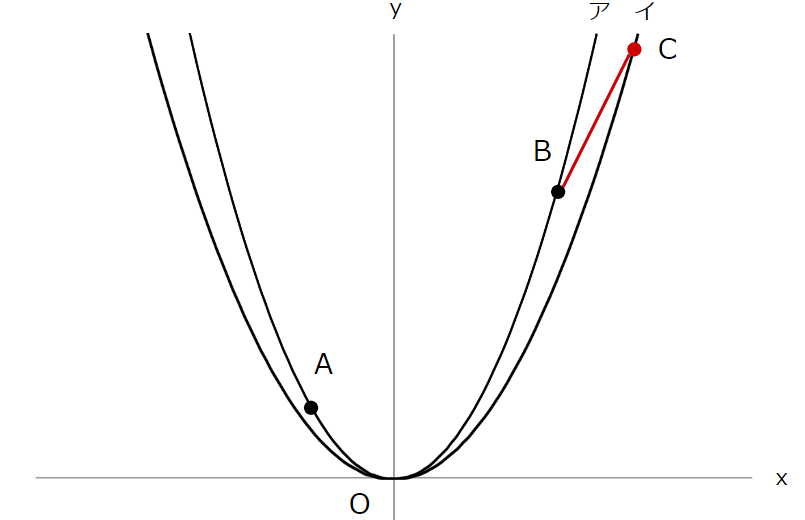
次に、点Cから \(x\) 軸に対して引いた垂線と、点Bを通る \(y\) 軸に対する垂線との交点をDとおき、直角三角形BCDをつくります。
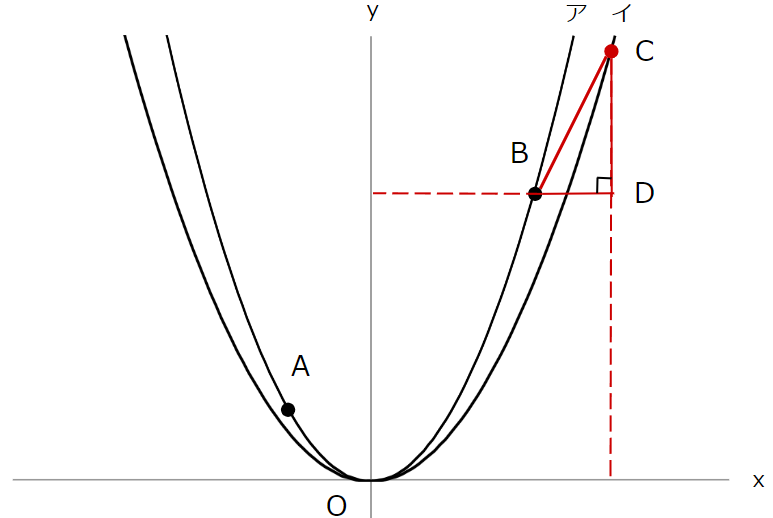
ここで、△BCDにおいて三平方の定理より、BC\(^2=\)CD\(^2+\)DB\(^2\) が成り立ちます。
最終的に求めたい線分BCの長さは、線分CDと線分DBの長さが分かれば出せそうです。
点Cは、イのグラフ上の点で \(x\) 座標が \(3\) と分かっているので、\(x=3\) をグラフの式 \(y=\dfrac{2}{3}x^2\) に代入して、
\(y=\dfrac{2}{3} \times 3^2=\dfrac{2}{3} \times 3 \times 3=6\)
これより、点Cの座標は \((3,6)\) となりますね。
次に、点Dの座標も考えてみましょう。
先ほどの図のように、 \(x\) 座標は点C、\(y\) 座標は点Bとそれぞれ同じなので、座標は \((3,4)\) です。
線分CDは、(点Cの \(y\) 座標) ー (点Dの \(y\) 座標) で求められるので、\(6-4=2 \ (cm)\)
同様にして、(線分DBは、点Dの \(x\) 座標 ー 点Bの \(x\) 座標) で求められるので、\(3-2=1 \ (cm)\)
それぞれを、BC\(^2=\)CD\(^2+\)DB\(^2\) に代入して、
BC\(^2=2^2+1^2=4+1=5\)
BC\(\gt 0\) なので、 BC\(=\sqrt5\) となります。
ポイント
・与えられている情報から、分からない座標を求めます
・三平方の定理を利用して、三角形の辺の長さを出します
(3)
アのグラフ上に,\(x\) 座標が正で,\(y\) 座標が \(1\) である点Pをとる。イのグラフ上に,\(x\) 座標が \(-1\) より小さく,\(y\) 座標が \(4\) である点Qをとる。四角形APBQの面積が \(12cm^2\) になるとき,\(a\) の値を求めなさい。【一部改題】
答え
\(a = \dfrac{1}{4}\)
解き方
問題文にあるように、点Pと点Qを書き加えて
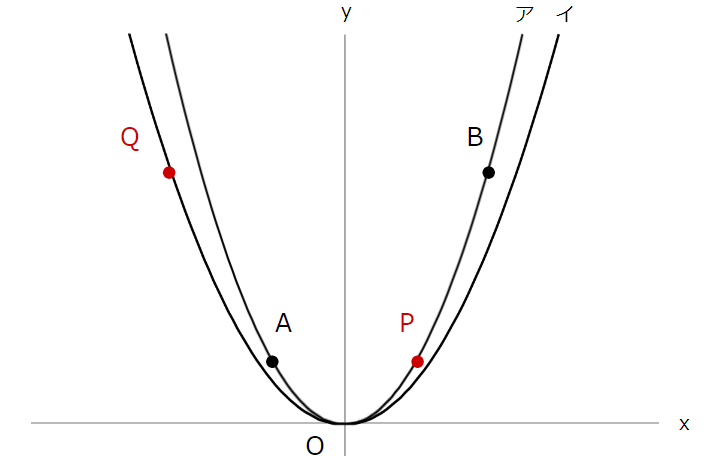
4点を結ぶと、下のような四角形ができあがります。
この面積が \(12cm^2\) になるときの \(a\) の値を求める、というのが今回の問題です。
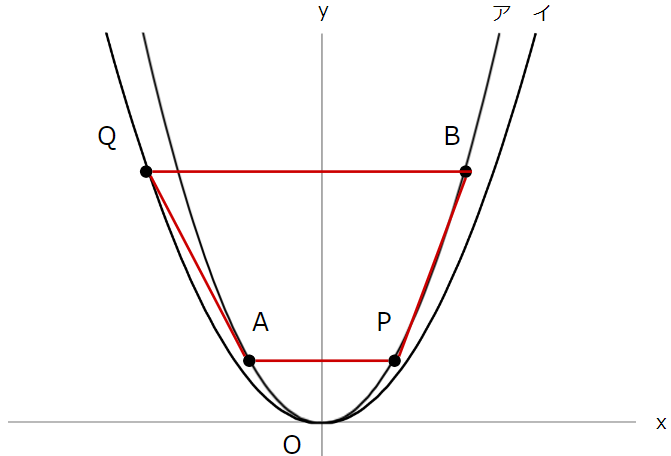
まず、4つの点の座標を整理しておきましょう。
点Aと点Bはすでに分かっていて、それぞれ \((-1,1)\) と \((2,4)\)
点Pはアのグラフ上にあって、\(x\) 座標が正、\(y\) 座標が \(1\) なので、アの式に代入して、
\(1=x^2\)
\(x \gt 0\) より、\(x=1\) と分かるので、座標は \((1,1)\)
点Qはイのグラフ上にあって、\(x\) 座標は \(-1\) より小さく、\(y\) 座標は \(4\) なので、イの式に代入して、
\(4=ax^2\)
両辺を \(a (\neq 0)\) で割って、右辺と左辺を入れ替えると、
\(x^2=\dfrac{4}{a}\)
\(x \lt 0\) なので、
\(x = -\sqrt{\dfrac{4}{a}}\)
これより、座標は \((-\sqrt{\dfrac{4}{a}},4)\) と分かります。
座標を整理すると、AとP、BとQの \(y\) 座標がそれぞれ同じことが見えてきます。
このとき、AP// BQ が成り立つので、四角形APBQは台形です。
ここからは、台形の面積の公式「((上底)\(+\)(下底))\(\times\)(高さ)\(\div\)2」を用いて考えましょう。
上底を辺BQ、下底を辺APとみなします。
辺の長さは、どちらも点の \(x\) 座標の絶対値の和で求めることができます。
点B、点Qの \(x\) 座標は、それぞれ \(2,-\sqrt{\dfrac{4}{a}}\) だから、辺BQは、\(2+\sqrt{\dfrac{4}{a}}(cm)\)
点A、点Pの \(x\) 座標は、それぞれ \(-1,1\) だから、辺APは、\(1+1=2(cm)\)
高さについては、点Aと点Bの \(y\) 座標の差で求められるので、\(4-1=3(cm)\)
これらを台形の面積の公式に代入して、
\(((2+\sqrt{\dfrac{4}{a}})+2) \times 3 \div 2\)
\(=(4+\sqrt{\dfrac{4}{a}}) \times 3 \div 2\)
台形の面積は \(12cm^2\) だから、
\(\begin{eqnarray}
(4+\sqrt{\dfrac{4}{a}}) \times 3 \div 2 &=& 12 \\[5pt]
(4+\sqrt{\dfrac{4}{a}}) \times 3 &=& 24 \\[5pt]
4+\sqrt{\dfrac{4}{a}} &=& 8 \\[5pt]
\sqrt{\dfrac{4}{a}} &=& 4 \\[5pt]
\sqrt{\dfrac{4}{a}} &=& \sqrt{16} \\[5pt]
\dfrac{4}{a} &=& 16 \\[5pt]
4 &=& 16a \\[5pt]
16a &=& 4 \\[5pt]
a &=& \dfrac{\bcancel 4}{\bcancel 16} \\[5pt]
a &=& \dfrac{1}{4} \end{eqnarray}\)
これは、\(0 \lt a \lt 1\) という条件を満たしているので、答えとして適当です。
ポイント
・問題に合わせて、点や線分を書き加えます
・点の座標を求めた上で、図形の面積を考えます。面積を求める公式が使えないどうか、合わせて検討してみましょう
Ⅱ
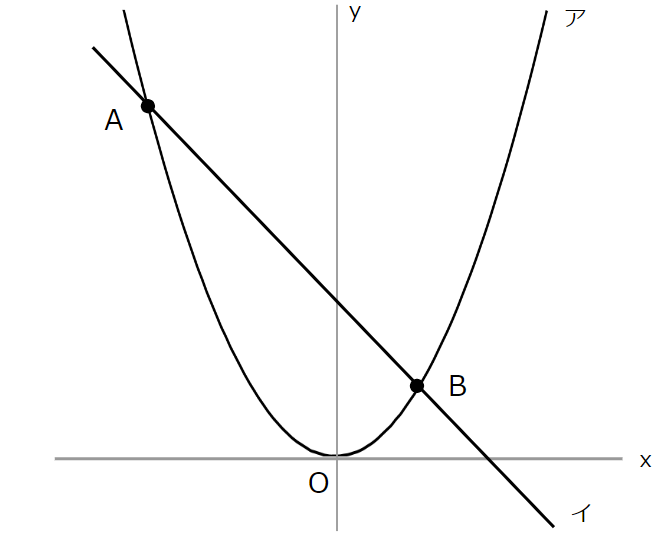
次の図において,アは関数 \(y=\dfrac{1}{2}x^2\),イは関数 \(y=-x+4\) のグラフであり,点Aの座標は \((-4,8)\),点Bの座標は \((2,2)\) である。アのグラフ上に、\(x\) 座標が \(t\) である点Pをとり,イのグラフ上に,点Pと \(x\) 座標が等しい点Qをとる。原点Oから \((0,1)\),\((1,0)\) までの距離を,それぞれ \(1cm\) とする。次の(1),(2)の問いに答えなさい。【一部改題】
(1)
\(t=-2\) のとき,2点A,Pを通る直線の式を求めなさい。求める過程も書きなさい
答え&解き方
求める直線は、2点A \((-4,8)\)、P\((-2,2)\) を通るので、傾きは、
\(\dfrac{2-8}{(-2)-(-4)}-3\)
したがって、求める直線は \(y=-3x+b\) と表すことができる。
この直線は、点A \((-4,8)\) を通るから、 \(y=-3x+b\) に \(x=-4,y=8\) を代入すると、
\(8=-3 \times (-4) +b\)
これを解くと、\(b=-4\)
よって、求める直線の式は \(y=-3x-4\)
ポイント
・問題文にあてはまるように点や線分を書き加えます
・最初にPの \(y\) 座標を求めます
・2点の座標を用いて、グラフの傾きと切片を出します
(2)
\(-4 \lt t \lt 2\) とする。
①
AQ\(=5 \sqrt{2} cm\) になるとき,\(t\) の値を求めなさい。
答え
\(t=1\)
解き方
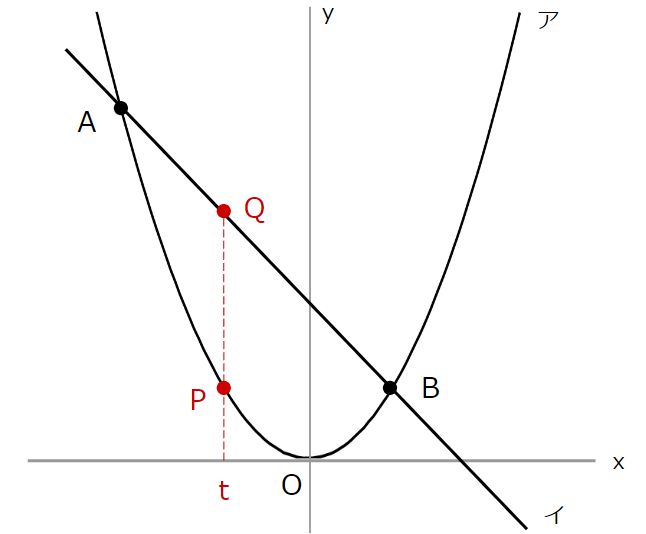
まず、下のように点を書き加えます。
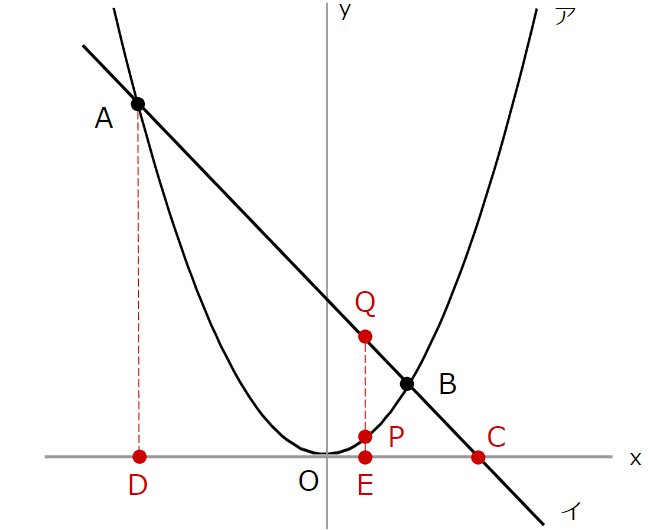
点Cは イと \(x\) 軸の交点、点Dは 点Aと \(x\) 座標が同じである \(x\) 軸上の点、点Eは 点Qと \(x\) 座標が同じである \(x\) 軸上の点、点P、Qは問題文にある通り、どちらも \(x\) 座標が \(t\) の点です。
また、それぞれの座標は以下の通りです。
点A:\((-4,8)\)
点B:\((2,2)\)
点C:\((4,0)\)
点D:\((-4,0)\)
点E:\((t,0)\)
点P:\((t,\dfrac{1}{2}t^2)\)
点Q:\((t,-t+4)\)
△ADCにおいて、
DC\(=\)OC\(+\)OD\(=4+4=8=\)AD
\(\angle\)ADC\(=90^{\circ}\)
だから、この三角形は斜辺をACとする直角二等辺三角形だといえます。
これより、AD:AC\(=1:\sqrt{2}\) なので、AC\(8\sqrt{2}\)
QC\(=\)AC\(-\)AQ\(=8\sqrt{2}-5\sqrt{2}=3\sqrt{2}\)
△ADCと△QECにおいて
\(\angle\)ADC\(= \angle\)QEC\(=90^{\circ} \cdots ①\)
また、AD//QE であり、平行線の同位角は等しいから、
\(\angle\)ADC\(= \angle\)QEC\(\cdots ②\)
①、②より2組の角がそれぞれ等しいから、△ADC \(\backsim\) △QECであり、△QECは直角二等辺三角形だと分かります。
これより、
EC:QC\(=1:\sqrt{2}\)
EC:\(3\sqrt{2}=1:\sqrt{2}\)
よって、EC\(=3\)
最終的に求めたい \(t\) は、OEと等しい値です。
OE\(=\)OC\(-\)EC\(=4-3=1\) より、\(t=1\) となります。
ポイント
・考えやすいように、図に点を書き足します
・直角二等辺三角形の性質を利用して、辺の長さを求めます
②
イのグラフ上に,\(x\) 座標が \(2\) より大きい点Rを,線分BRの長さと線分BQの長さが等しくなるようにとる。アのグラフ上に,点Rと \(x\) 座標が等しい点Sをとる。四角形PQRSの面積が \(30cm^{2}\) になるとき,\(t\) の値を求めなさい。
答え
\(t = 2- \sqrt{5}\)
解き方
最初に、下の図のように点を書き加えておきます。
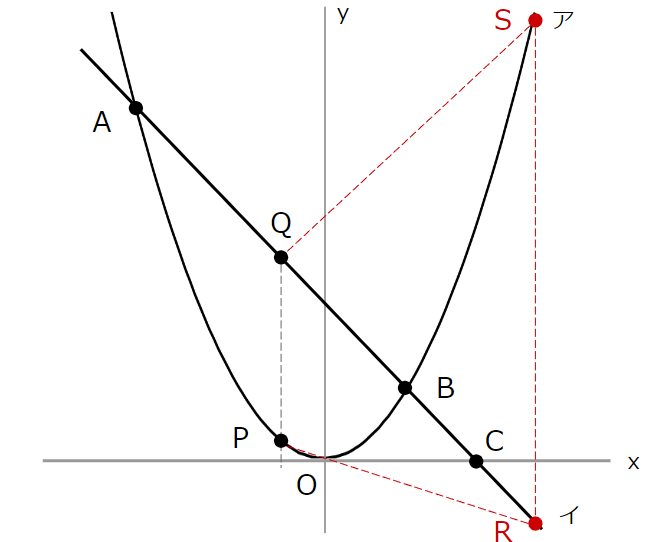
BはQRを二等分する点だから、Rの座標は \((4-t,t)\) と表すことができます。
Sは、Rと \(x\) 座標が同じで、アのグラフ上の点なので、\(y=\dfrac{1}{2}(4-t)^2\) となります。
ここまで整理すると、下のようになります。
点P:\((t,\dfrac{1}{2}t^2)\)
点Q:\((t,-t+4)\)
点R:\((4-t,t)\)
点S:\((4-t,\dfrac{1}{2}(4-t)^2)\)
四角形PQRSは PQ//RS の台形なので、面積の公式「((上底)\(+\)(下底))\(\times\)(高さ)\(\div\)2」を用いて考えることができます。
PQを上底、RSを下底、QRとRSの距離を高さとみて、それぞれの長さを求めます。
PQ\(=-t+4-(\dfrac{1}{2}t^2)=-\dfrac{1}{2}t^2-t+4\)
RS\(=\dfrac{1}{2}(4-t)^2-t = \dfrac{1}{2}(16-8t+t^2)-t=\dfrac{1}{2}t^2-5t+8\)
これより、
PQ\(+\)RS\(=(-\dfrac{1}{2}t^2-t+4)+(\dfrac{1}{2}t^2-5t+8)=-6t+12\)
また、高さは \(4-t-t=-2t+4\)
四角形PQRSの面積は \(30cm^{2}\) なので、ここまで求めた長さを公式に代入すると、
\(\begin{eqnarray}
(-6t+12) \times (-2t+4) \div 2 &=& 30 \\[5pt]
6(-t+2) \times 2(-t+2) &=& 60 \\[5pt]
12(-t+2)^2 &=& 60 \\[5pt]
(-t+2)^2 &=& 5 \\[5pt]
-t+2 &=& \pm \sqrt{5} \\[5pt]
t &=& 2 \pm \sqrt{5} \end{eqnarray}\)
\(t\) は \(2\) より小さいので、答えは \(t = 2- \sqrt{5}\)
ポイント
・必要な点や線分を書き加えます
・文字を使って、それぞれの座標を表します
・面積を求める公式に分かっている数値をあてはめて、方程式を解きます

