秋田県高校入試「数学」大問3の解答・解説です。
入試の概要や他の問題を確認したい方は、下の記事をご覧ください。
なお、実際の入試問題や解答は、以下のサイトでご覧いただけます。

※問題や解説に登場する図やグラフは、すべて当サイトのデザイナーが作成したものです
大問3
A中学校の図書委員会は,全校生徒を対象として,ある日曜日の読書時間を調査した。次の(1)~(3)の問いに答えなさい。
(1)
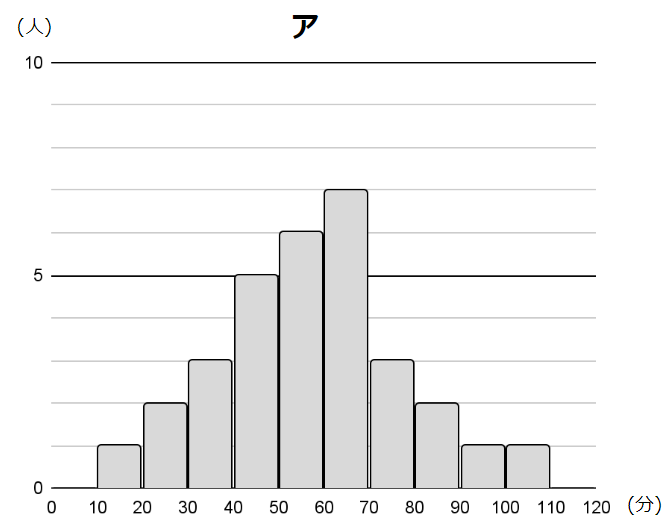
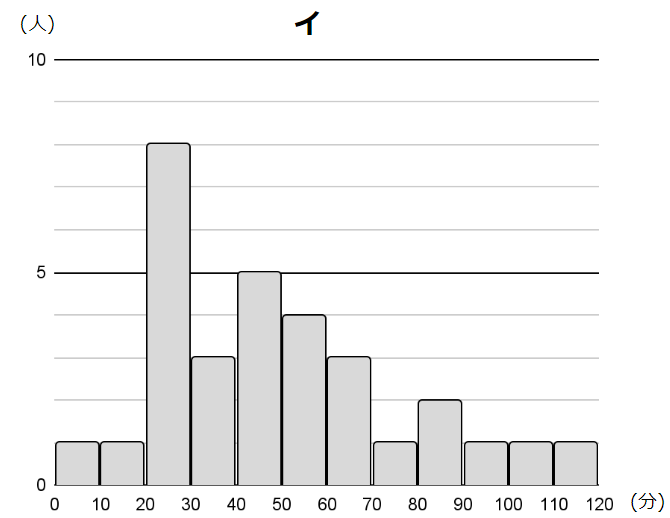
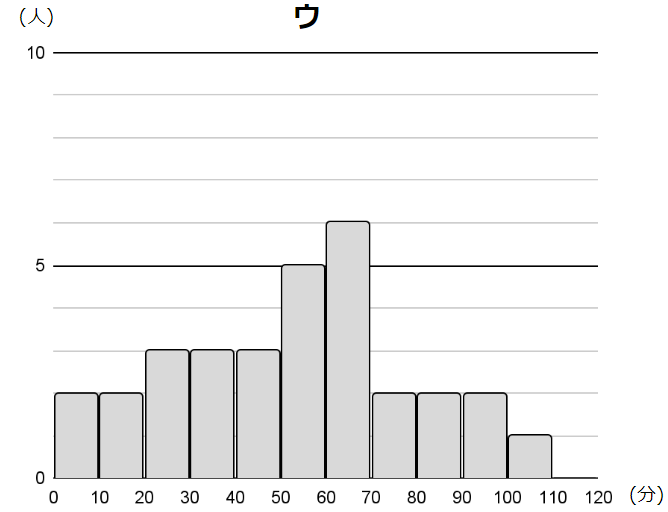
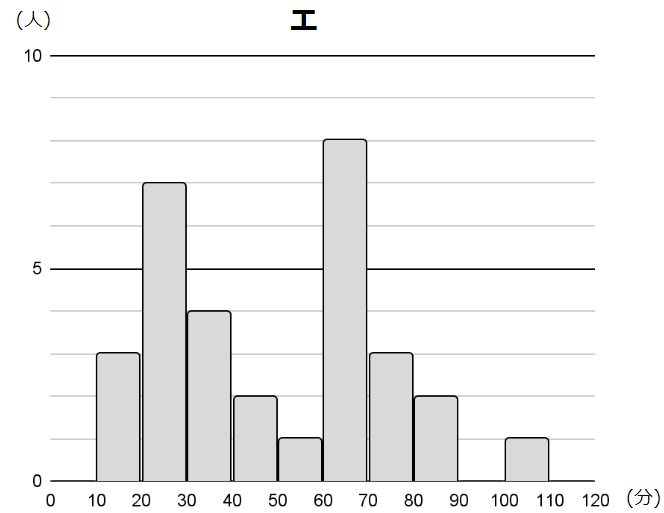
図1のア~エは,3年1組を含む4つの学級の読書時間のデータを,ヒストグラムに表したものである。例えば,アの10~20の階級では,読書時間が10分以上20分未満の生徒が1人いることを表している。4つの学級の生徒数は,すべて31人である。
3年1組のヒストグラムは,最頻値が中央値よりも小さくなる。3年1組のヒストグラムとして最も適切なものを,図1のア~エから1つ選んで記号を書きなさい。
図1
答え
イ
解き方
ア~エの中から、3年1組のヒストグラムを選ぶ問題です。
3年1組のヒストグラムの特徴として「最頻値が中央値よりも小さくなる」ことが挙げられているので、グラフそれぞれの最頻値と中央値を調べてみることにします。
まず、最頻値から求めてみましょう。
アから順に、最頻値は65、25、65、65です。
次に中央値ですが、どのグラフも31人のデータで構成されているので、小さい値(もしくは大きい値)から数えて16人目のデータが中央値になります。
これを踏まえると、アから順に、55、45、55、45ですね。
この中で、唯一(最頻値)<(中央値)となっているヒストグラム(イ)が正解です。
今回は最頻値と中央値の両方を求めましたが、最頻値を求めるだけでも答えは出せそうです。最頻値をみると、イだけが他と比べて明らかに値が小さくなっています。
ポイント
・グラフから最頻値や中央値を正確に読み取ります
・データの代表値(最頻値・中央値・平均値など)の意味を理解しておく必要があります
(2)
次の表は,3年2組30人の読書時間のデータを,小さい順に並べたものである。このデータの範囲と第1四分位数をそれぞれ求めなさい。
3年2組の読書時間(単位 分)

答え
範囲…105分、第1四分位数…30分
解き方
最初に、データの範囲を求めます。
範囲は(最大値)ー(最小値)で計算できます。
3年2組の読書時間で最も長いのは110分、最も小さいのは5分なので、範囲は
110ー5=105 (分)
次に、第1四分位数を求めていきましょう。
まずは、データの値の大きさで上位と下位の2つに分けます。
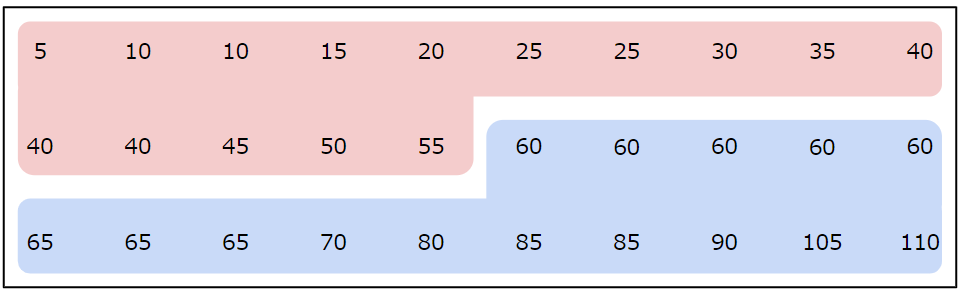
注目するのは下位15個のデータです。
この15個のデータの中央値、つまり、小さい値(もしくは大きい値)から数えて8つ目のデータが第1四分位数にあたります。
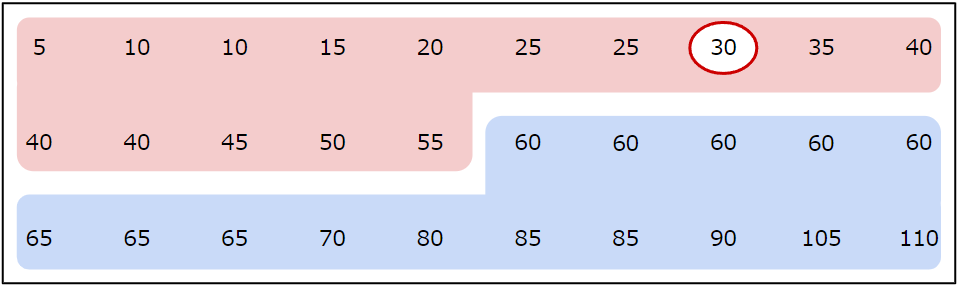
よって、第1四分位数は30(分) です。
ポイント
・範囲や第1四分位数の求め方を押さえておきます
・与えられた表に印をつけたり、囲みを入れたりすると、データが見やすくなります
(3)
3年1組,2組,3組で運動部に所属している生徒は,16人ずついる。図2は,3年1組の運動部の生徒をグループ1,3年2組の運動部の生徒をグループ2,3年3組の運動部の生徒をグループ3とし,それぞれの読書時間のデータを,箱ひげ図に表したものである。
図2
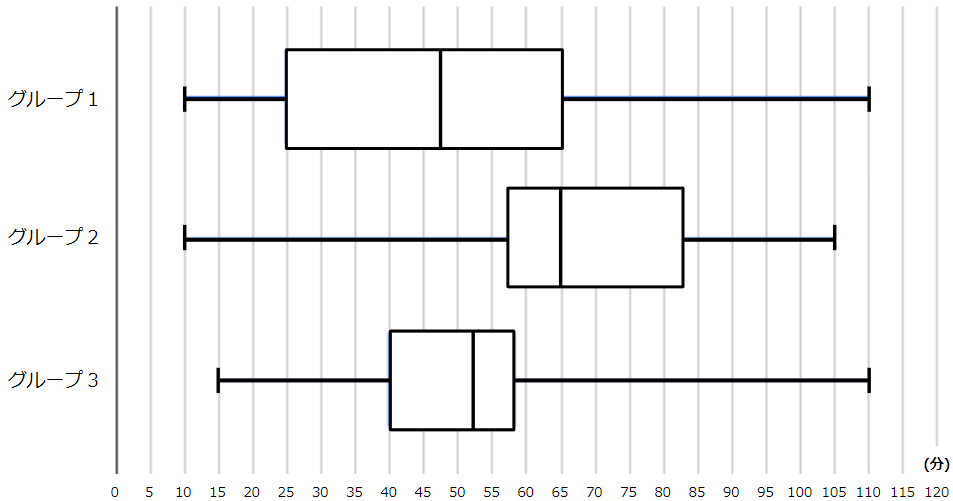
①
図2から読み取れることとして正しいものを,次のア~エからすべて選んで記号を書きなさい。
ア 読書時間が55分以下の生徒数が最も少ないグループは,グループ2である。
イ 読書時間が55分以上の生徒数が最も多いグループは,グループ3である。
ウ どのグループにも,読書時間が80分以上100分未満の生徒は必ずいる。
エ どのグループにも,読書時間が100分以上の生徒は必ずいる。
答え
ア、エ
解き方
箱ひげ図に表現されているのは、最小値・第1四分位数・第2四分位数(中央値)・第3四分位数・最大値の5つです。
このうち、第1四分位数は全体の25%、第2四分位数(中央値)は全体の50%、第3四分位数は全体の75%にあたる値を表す言葉です。
3つのグループとも16人なので、最小値から中央値までに8人、中央値から最大値までに8人のデータがあることが分かります。言い換えると、中央値を境に、下位8つと上位8つに分けられるということです。
また、下位8人のデータの中央値が第1四分位数、上位8人のデータの中央値が第3四分位数にあたります。
ここまでの話をまとめたのが下の図です。
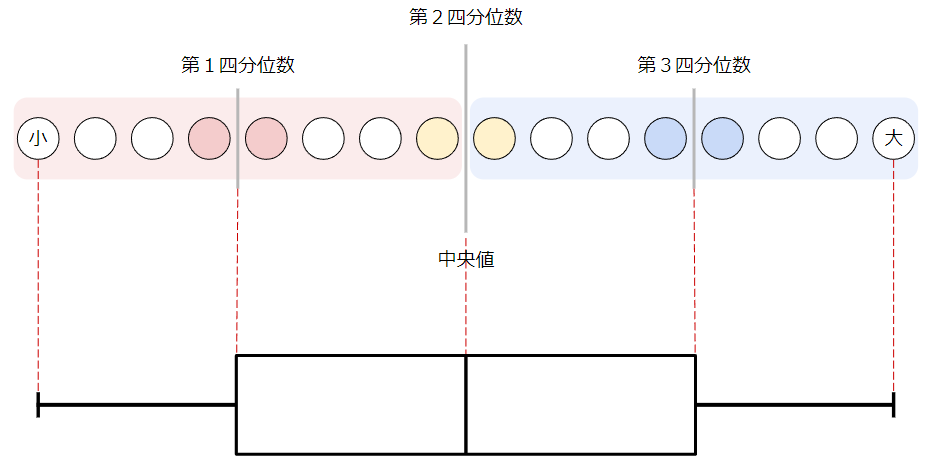
これを踏まえた上で、選択肢を一つひとつ見ていきましょう。
ア 読書時間が55分以下の生徒数が最も少ないグループは,グループ2である。
ループ1では、中央値と第3四分位数の間に55分のめもりがあります。このことから、少なくとも8人の読書時間は55分以下だと分かります。
グループ2では、最小値と第1四分位数の間に55分のめもりがあります。このことから、多くて4人の読書時間は55分以下だと分かります。
グループ3では、グループ1と同様に中央値と第3四分位数の間に55分のめもりがあります。このことから、少なくとも8人の読書時間は55分以下だと分かります。
よって、読書時間が55分以下の生徒が最も少ないのはグループ2です。
イ 読書時間が55分以上の生徒数が最も多いグループは,グループ3である。
グループ1では、中央値と第3四分位数の間に55分のめもりがあります。このことから、少なくとも4人の読書時間は55分以上だと分かります。
グループ2では、最小値と第1四分位数の間に55分のめもりがあります。このことから、少なくとも12人の読書時間は55分以上だと分かります。
グループ3では、グループ1と同様に中央値と第3四分位数の間に55分のめもりがあります。このことから、少なくとも4人の読書時間は55分以上だと分かります。
よって、読書時間が55分以上の生徒が最も多いのはグループ2です。
ウ どのグループにも,読書時間が80分以上100分未満の生徒は必ずいる。
グループ1は、第3四分位数と最大値の間に上の範囲があります。箱ひげ図から、第3四分位数を65分、最大値を110分と読み取って考えてみることにしましょう。
この範囲には4人の生徒がいますが、うち一人の読書時間は最大値の110分です。ここで、他の3人の読書時間が65分・70分・75分だとすると、先ほどの条件を満たします。
しかし、これは「どのグループにも、読書時間が80分以上100分未満の生徒は必ずいる」ことには反するので、ウは正しくないことが分かります。
エ どのグループにも,読書時間が100分以上の生徒は必ずいる。
それぞれのグループの最大値に注目してみます。
アは110分、イは105分、ウは110分と読み取れるので、どのグループにも読書時間が100分以上の生徒が必ずいると分かります。
ポイント
・四分位数の意味と、箱ひげ図との関係性を理解しておきます
②
図2において,読書時間のデータの散らばりぐあいが最も大きいグループを,次のア~ウから1つ選んで記号を書きなさい。また,そのように判断した理由を,「範囲」と「四分位範囲」という両方の語句を用いて書きなさい。
ア グループ1 イ グループ2 ウ グループ3
答え
記号:ア
理由:範囲と四分位範囲が、ともに最も大きいから。
解き方
データの散らばりぐあいは、範囲や四分位範囲を求めることで分かります。
範囲は(最大値)ー(最小値)、四分位範囲は(第3四分位数)ー(第1四分位数)で求めることができます。
ここで、それぞれのグループの最小値・第1四分位数・第3四分位数・最大値を順によみとっていくと、
グループ1は、順に10分・25分・65分・110分
グループ2は、順に10分・57.5分・82.5分・105分
グループ3は、順に15分・40分・57.5分・110分
ここから、それぞれの範囲と四分位範囲を求めると、
グループ1は、110-10=100(分) と 65-25=40(分)
グループ2は、105-10=95(分) と 85.5-57.5=25(分)
グループ3は、110-15=95(分) と 57.5-40=17.5(分)
範囲と四分位範囲が大きいほど、散らばりぐあいも大きくなるので、答えはグループ1。
ポイント
・指定された言葉を必ず使って、選択肢を選んだ理由を書きます
・データの散らばりは、範囲と四分位範囲に注目して考えます

