秋田県高校入試「数学」大問2の解答・解説です。
入試の概要や他の問題を確認したい方は、下の記事をご覧ください。
なお、実際の入試問題や解答は、以下のサイトでご覧いただけます。

※問題や解説に登場する図やグラフは、すべて当サイトのデザイナーが作成したものです
大問2
(1)
駅から \(3600 \ m\) 離れた図書館まで,まっすぐで平らな道がある。健司さんは,午前10時に駅を出発し,毎分 \(60 \ m\) の速さで図書館に歩いて向かった。駅から \(1800 \ m\) 離れた地点で立ち止まって休憩し,休憩後は毎分 \(120 \ m\) の速さで図書館に走って向かい,午前10時50分に図書館に着いた。次の図は,健司さんが駅を出発してから \(x\) 分後に,駅から \(y \ m\) 離れた地点にいるとして,\(x\) と \(y\) の関係を表したグラフの一部である。
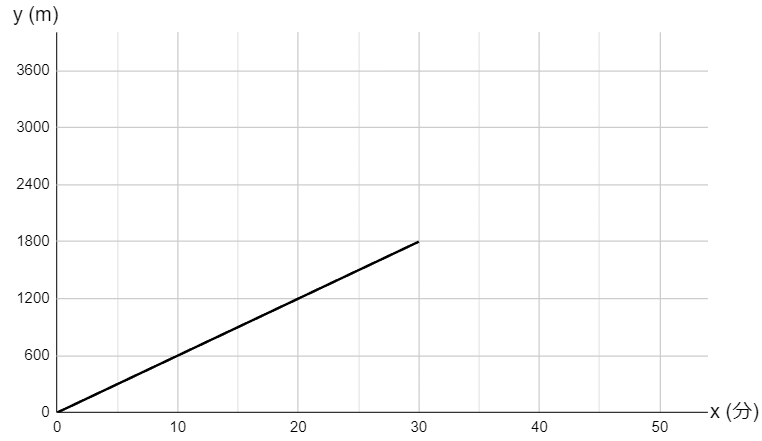
①
健司さんが駅から \(1800 \ m\) 離れた地点で休憩を始めてから,図書館に着くまでの \(x\) と \(y\) の関係を表したグラフを,図にかき加えなさい。
答え
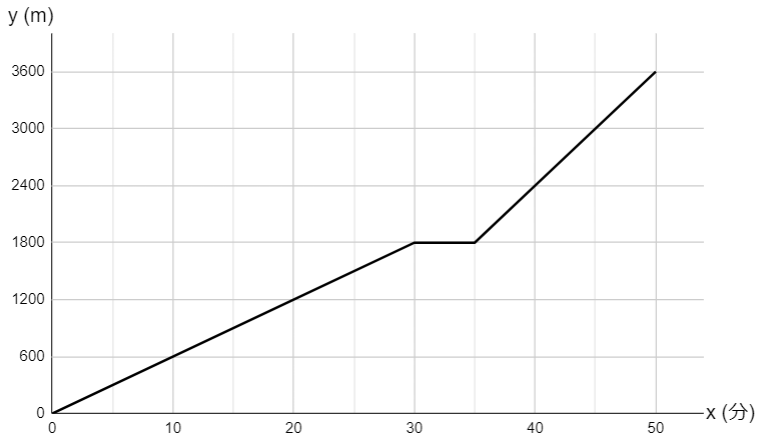
解き方
駅から図書館までの距離は \(3600 \ m\) で、健司さんが休憩した場所は駅から \(1800 \ m\) 離れた地点にあるから、健司さんが休憩した場所から駅までの距離は、\(3600-1800=1800 (m)\) です。
健司さんは、この距離を毎分 \(120 \ m\) の速さで走って進んだので、かかる時間は、\(1800 (m) \div 120(m/分)=15(分)\) 。
健司さんは、午前10時50分に図書館に着き、休憩場所から図書館まで \(15\) 分かかったことから、午前10時35分に休憩場所を発ったことが分かります。
これは、グラフでは \((x,y)=(35,1800)\) の点にあたりますね。
与えられたグラフの \((x,y)=(35,1800)\) 、そして \((x,y)=(50,3600)\) に点を打ち直線で結ぶと、図が完成します。
ポイント
・傾きや切片を求めて、グラフの式をつくります
・複数のグラフの交点の座標は、連立方程式を解くことで求められます
②
健司さんの姉の美咲さんは,健司さんが駅を出発した時刻と同じ時刻に,自転車に乗って図書館を出発し,毎分 \(240 \ m\) の速さで駅に向かっていたところ,歩いて図書館に向かう健司さんと出会った。美咲さんと健司さんが出会ったときの時刻を求めなさい。
答え
10時12分
解き方
美咲さんが、図書館から駅に向かったときの \(x\) と \(y\) の関係をグラフに表してみます。
図書館から駅までの距離は問題文より \(3600 \ m\)、美咲さんは毎分 \(240 \ m\) で進んだから、かかった時間は
\(3600(m) \div 240(m/分)=15(分)\)
これより、美咲さんのグラフは \((x,y)=(0,3600), (15,0)\) を通ることが分かります。
先ほどのグラフに書き加えると、下のようになりますね。
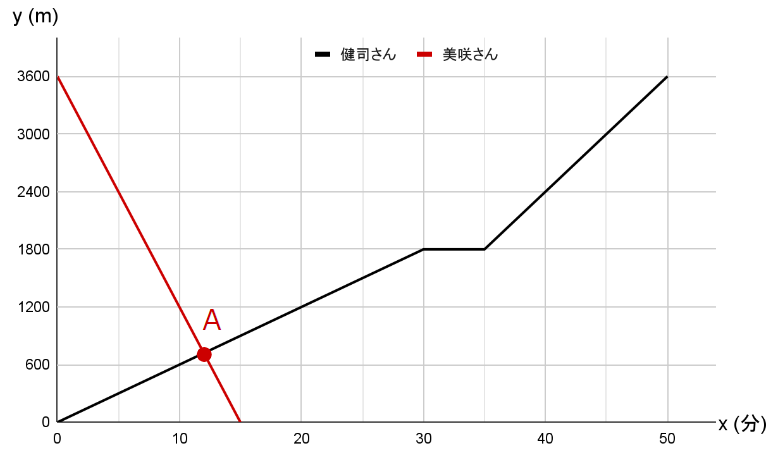
健司さんのグラフと交わっているところ(交点Aと置きます)、ここが健司さんと美咲さんが出会う地点です。最終的に求めたい「美咲さんと健司さんが出会ったときの時刻」は、この交点の \(x\) 座標から求めることができます。
では、交点Aを有する健司さんと美咲さんのグラフ、それぞれを式に表してみましょう。
健司さんのグラフから考えてみます。毎分 \(60 \ m\) の速さで図書館に歩いて向かったとあるので、傾きは \(60\) と分かります。また、グラフは原点を通る比例のグラフだから、式は \(y=60x\) と表されます。
同じように、美咲さんは毎分 \(240 \ m\) で健司さんと逆向きに進んでいるので、傾きは \(-240\)。切片は \(3600\) だから、式は \(y=-240x+3600\) と表されます。
この交点Aは、2つの式を連立方程式にして解くことで求めることができます。
2つの式より、
\(60x = -240x+3600\)
これを解いて、
\(\begin{eqnarray}
60x+240x &=& 3600 \\[5pt]
300x &=& 3600 \\[5pt]
x &=& 12 \end{eqnarray}\)
これで二人が出会うのは、健司さんが家を出てから \(12\) 分後と分かります。
よって、求める時刻は10時12分となります。
ポイント
・割り算から先に計算します
・マイナスを含む計算なので注意が必要です
(2)
次の図のように,袋Aには整数1,2,3が1つずつ書かれた3枚のカードが,袋Bには整数4,5,6が1つずつ書かれた3枚のカードが入っている。このとき,下の①,②の問いに答えなさい。
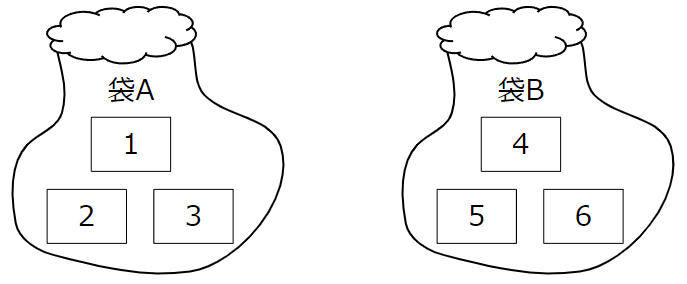
①
袋A,袋Bからそれぞれカードを1枚ずつ取り出し,取り出されたカードに書かれている数の積を求める。このとき,積が奇数になる確率を求めなさい。ただし,袋Aからどのカードが取り出されることも,袋Bからどのカードが取り出されることも,それぞれ同様に確からしいものとする。
答え
\(\dfrac{2}{9}\)
解き方
袋A、Bそれぞれから取る数の組み合わせと、取った数の積をまとめると、下のようになります。
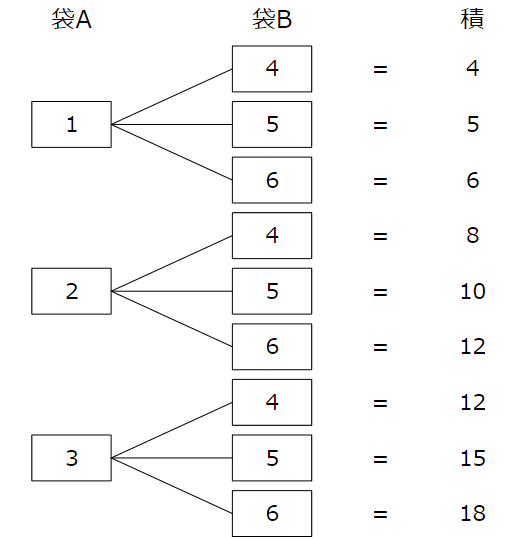
今回求めたいのは積が奇数になる確率なので、先ほどの図の中で積が奇数のものに印をつけてみます。
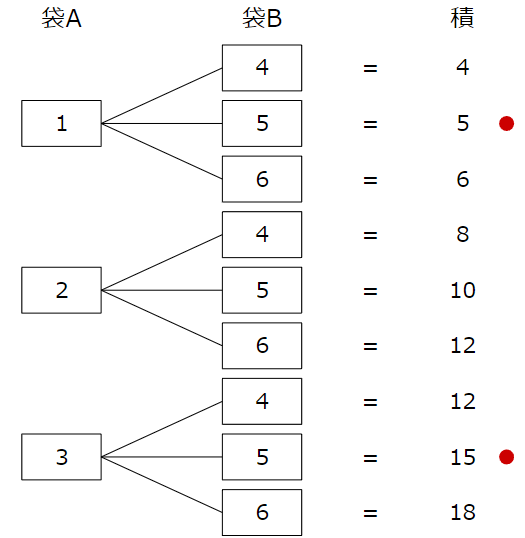
数の組み合わせは9通りある中で、積が奇数になるものは2通りと分かるので、求める確率は \(\dfrac{2}{9}\) です。
ポイント
・図や樹形図を書いて、全体で何通りの数の組み合わせがあるかを調べます
・積が奇数になるものを探してから確率を求めます
②
袋A,袋Bに入っているカードとは別に,整数7が書かれているカードが6枚ある。袋Bに,整数7が書かれているカードを何枚か追加し,袋A,追加したカードが入っている袋Bからそれぞれカードを1枚ずつ取り出し,取り出されたカードに書かれている数の積を求める。積が奇数になる確率と積が偶数になる確率が等しいとき,追加したカードは何枚か,求めなさい。ただし,袋Aからどのカードが取り出されることも,追加したカードが入っている袋Bからどのカードが取り出されることも,それぞれ同様に確からしいものとする。
答え
5枚
解き方
問題のイメージ図は、下の通りです。
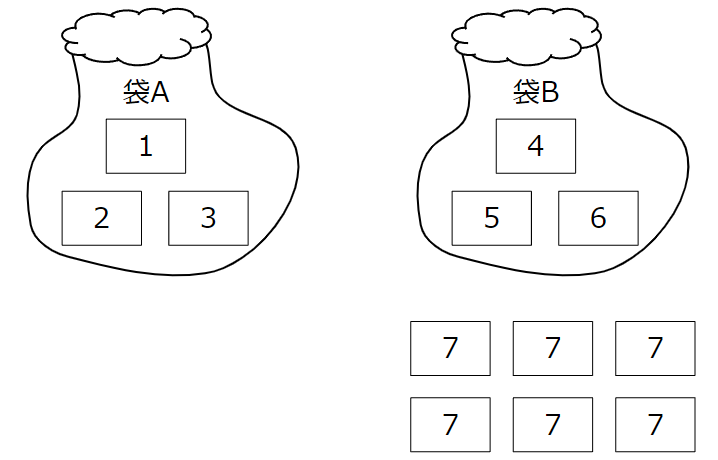
まず、袋Aの数字と「7」との組み合わせと、その積を整理しておきます。
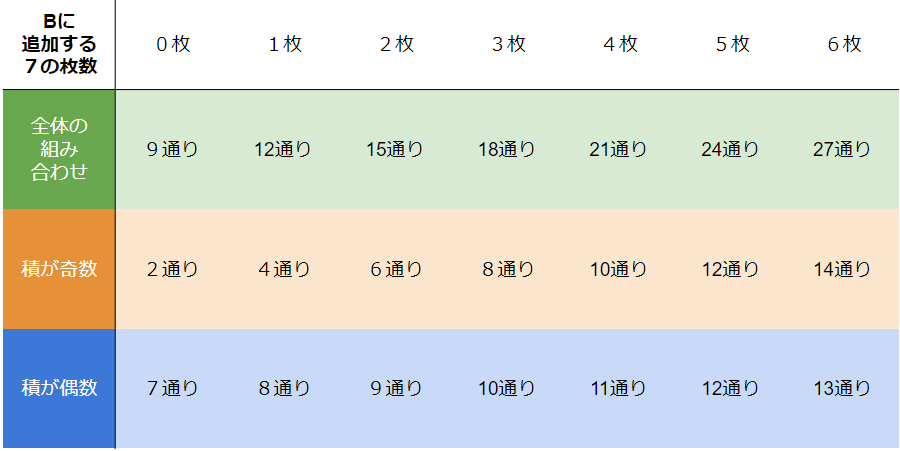
最終的に求めたいのは「積が奇数になる確率と積が偶数になる確率が等しいときの、袋Bに入れた7の枚数」ですね。
これは、先ほどの表を縦に見ていって、積が奇数、偶数の場合の数が同じになっている部分を探すと分かります。
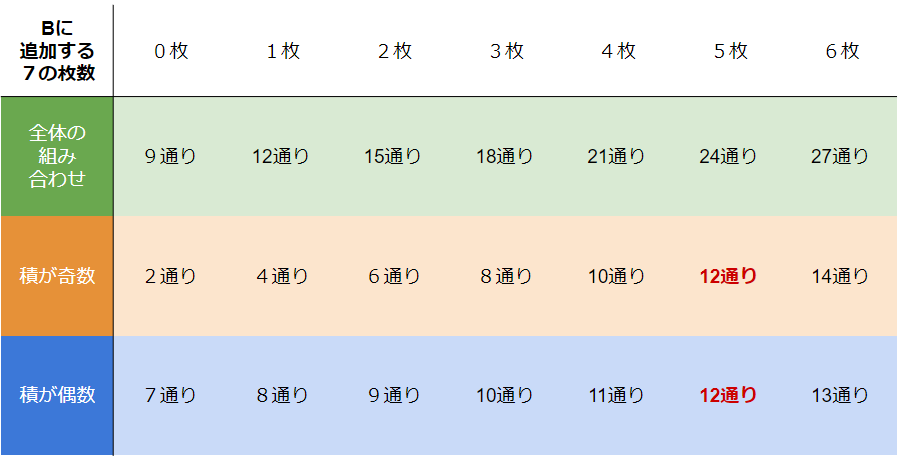
よって、答えは5枚です。
ポイント
・まずは、7を1枚追加したときどうなるかを考えます
・枚数を増やすと数の組み合わせがどう増えていくのかを、表や図にまとめてみると分かりやすいです(すべての場合を計算して出しても、もちろん構いません)
(3)
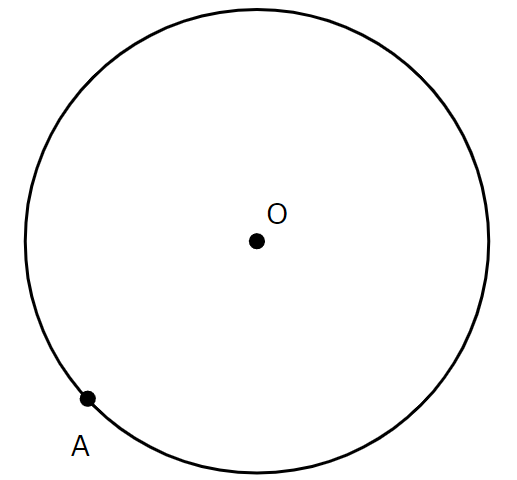
次の図のように,点Oを中心とする円の周上に点Aがある。このとき,点Aを接点とする円Oの接線を定規とコンパスを用いて作図しなさい。ただし,作図に用いた線は消さないこと。
答え
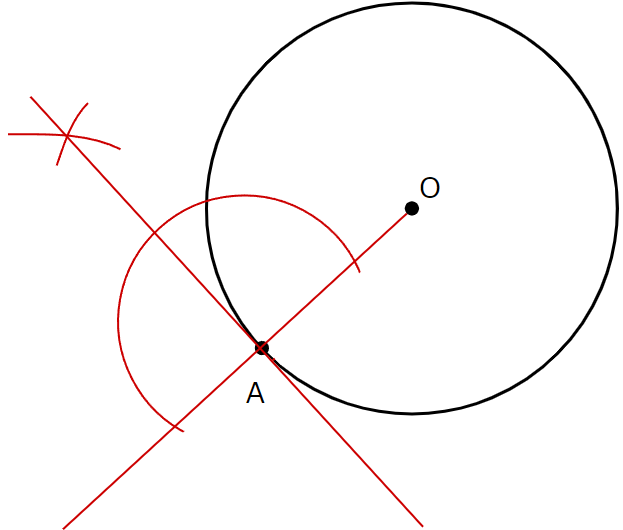
解き方
以下の手順で作図します。
①:半直線OAを引きます
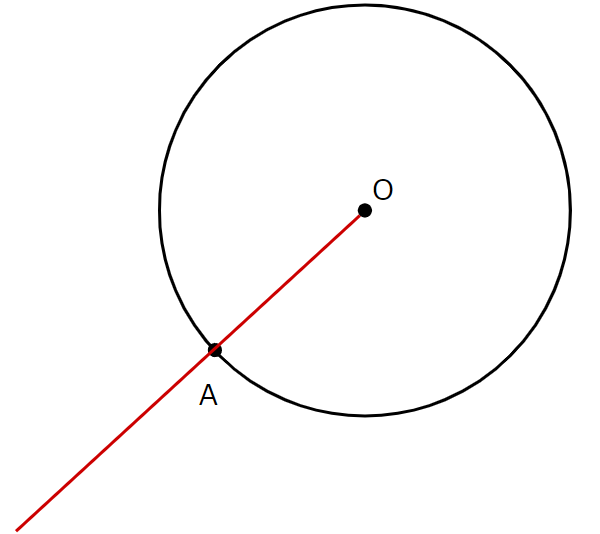
②:点Aにコンパスの針を置き、半円を描きます
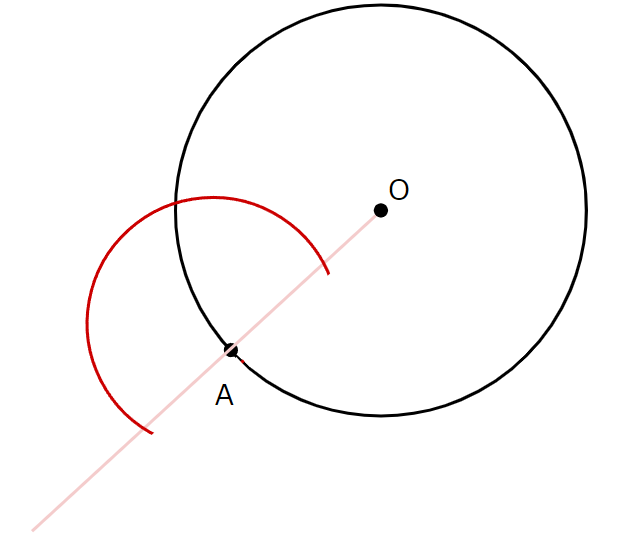
③:さきほどの半円と半直線OAとの交点にコンパスの針を置き、印をつけます
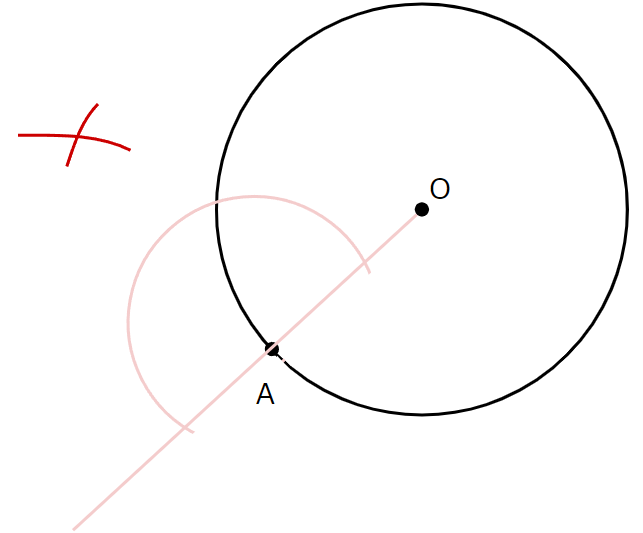
④:③でつけた印の交点とAを通る直線を引きます
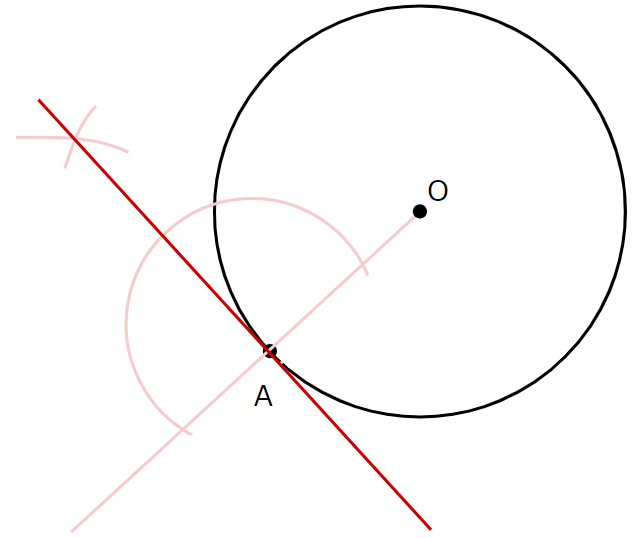
ポイント
・垂線の作図の仕方を身に付けておきます

