秋田県高校入試「数学」大問1の解答・解説です。
入試の概要や他の問題を確認したい方は、下の記事をご覧ください。
なお、実際の入試問題や解答は、以下のサイトでご覧いただけます。

※問題や解説に登場する図やグラフは、すべて当サイトのデザイナーが作成したものです
大問1
1
\(8+12\div(-4)\) を計算しなさい。
答え
\(5\)
解き方
途中式は次のようになります。
\(8+12\div(-4)\)
\(=8+(-3)\)
\(=5\)
ポイント
・割り算から先に計算します
・マイナスを含む計算なので注意が必要です
2
\(12ab\div6a^2\times2b\) を計算しなさい。
答え
\(\dfrac{4b^2}{a}\)
解き方
途中式は次のようになります。
\(12ab \div 6a^2 \times 2b\)
\(=\dfrac{12ab}{6a^2} \times 2b\)
\(=\dfrac{\bcancel{12}\bcancel{a}b}{\bcancel{6}a^\bcancel{2}} \times 2b\)
\(=\dfrac{2b}{a} \times 2b\)
\(=\dfrac{4b^2}{a}\)
ポイント
・左から順番に計算します
・同じ文字を消去することを忘れないようにしましょう
3
次の数の大小を,不等号を使って表しなさい。 \(4\), \(\sqrt{10}\)
答え
\(4 \gt \sqrt{10}\)
解き方
このままだと、数の大小を比べにくいので、\(4\) を ルートに直します。
\(4=\sqrt{16}\)
ここで2つの数を比べてみると、\(\sqrt{16} \gt \sqrt{10}\) となります。
よって、\(4 \gt \sqrt{10}\) が答えになります。
ポイント
・どちらもルートのついた数に直します
4
\(x=\dfrac{1}{2}\),\(y=-3\)のとき,\(2(x-5y)+5(2x+3y)\) の値を求めなさい。
答え
\(-9\)
解き方
\(2(x-5y)+5(2x+3y)\)
\(=2x-10y+10x+15y\)
\(=12x+5y\)
ここで、\(x=\dfrac{1}{2}\),\(y=-3\) をそれぞれ代入して
\(12 \times \dfrac{1}{2}+5 \times (-3) \)
\(=6-15\)
\(=-9\)
ポイント
・代入は、元の式ではなく、簡単にした式でおこないます
5
\(\dfrac{\sqrt{2}}{2}-\dfrac{1}{3\sqrt{2}}\) を計算しなさい。
答え
\(=\dfrac{\sqrt{2}}{3}\)
解き方
途中式は次のようになります。
\(\dfrac{\sqrt{2}}{2}-\dfrac{1}{3\sqrt{2}}\)
\(=\dfrac{\sqrt{2}}{2}-\dfrac{1 \times \sqrt{2}}{3\sqrt{2} \times \sqrt{2}}\)
\(=\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{6}\)
\(=\dfrac{3 \sqrt{2}}{6}-\dfrac{\sqrt{2}}{6}\)
\(=\dfrac{2 \sqrt{2}}{6}\)
\(=\dfrac{\bcancel 2 \sqrt{2}}{\bcancel 6}\)
\(=\dfrac{\sqrt{2}}{3}\)
ポイント
・有理化をします【途中式:2行目】
・通分をして計算をします【途中式:4行目】
6
方程式 \(\dfrac{5x-2}{4}=7\) を解きなさい。
答え
\(x=6\)
解き方
両辺に \(4\) をかけて
\(\begin{eqnarray}
\dfrac{5x-2}{4} \times 4 &=& 7 \times 4 \\[5pt]
\dfrac{5x-2}{\bcancel 4} \times \bcancel 4 &=& 7 \times 4 \\[5pt]
5x-2 &=& 28 \\[5pt]
5x &=& 28+2 \\[5pt]
5x &=& 30 \\[5pt]
x &=& 6 \end{eqnarray}\)
ポイント
・一次方程式の基本の解き方にそって、問題を解きます
・答えがでたら、最初の式に代入をして等式が成り立つか確かめましょう
7
連立方程式 \(\begin{eqnarray} \left\{ \begin{array}{l} 2x+y=5 \\ x-4y=7\end{array} \right. \end{eqnarray}\) を解きなさい。
答え
\(x=3, y=-1\)
解き方
まず、それぞれの式に番号を振ります。
\(\begin{eqnarray} \left\{ \begin{array}{l} 2x+y=5 \cdots ①\\ x-4y=7 \cdots② \end{array} \right. \end{eqnarray}\)
\(②\times 2\) を計算すると
\(2x-8y=14\)
\(①-② \times 2\) を計算して
\(\begin{array}{r}
2x+ \phantom{0} y = \phantom{0} 5 \\[-3pt]
\underline{-)2x-8y = 14}\\[-3pt]
9y = -9 \\[-3pt]
y = -1 \end{array}\)
これを\(①\)に代入して
\(\begin{eqnarray}
2x+(-1) &=& 5 \\
2x-1 &=& 5 \\
2x &=& 5+1 \\
2x &=& 6 \end{eqnarray}\)
両辺を3で割って
\(x=3\)
よって、答えは \(x=3, y=-1\)
ポイント
・文字の係数をそろえて、どちらかの値を先に求めます
・片方の文字が分かったら、代入してもう一方の値を求めます
8
方程式 \(x^2+5x+2=0\) を解きなさい。
答え
\(x= \dfrac{-5 \pm \sqrt{17}}{2}\)
解き方
解の公式に当てはめて
\(\begin{eqnarray}
x &=& \dfrac{-5\pm\sqrt{5^2-4 \times 2}}{2 \times 1} \\[5pt]
&=& \dfrac{-5\pm\sqrt{25-8}}{2} \\[5pt]
&=& \dfrac{-5\pm\sqrt{17}}{2} \end{eqnarray}\)
9
下の図のように,1辺の長さが \(5 cm\) の正三角形の紙を,その一部が重なるように,横一列に3枚並べて図形をつくる。このとき,重なる部分は,すべて1辺の長さが \(a cm\) の正三角形となるようにする。図の太線は,図形の周囲を表している太線で表した図形の周囲の長さを,\(a\) を用いた式で表しなさい。【一部改題】
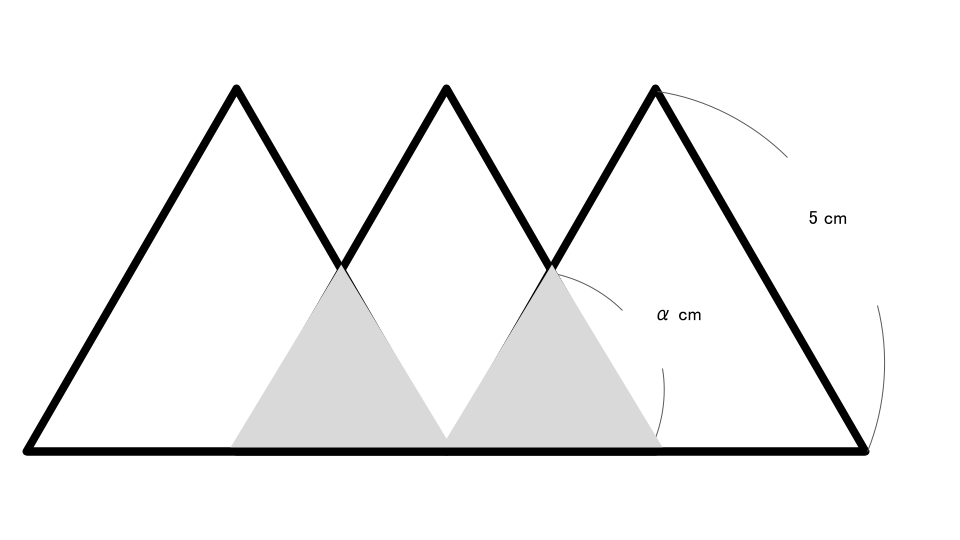
答え
\((45-6a) \ cm\)
解き方
図形の周囲は、下図のように赤色・黄色・青色の3種類の長さの異なる辺から成り立っています。
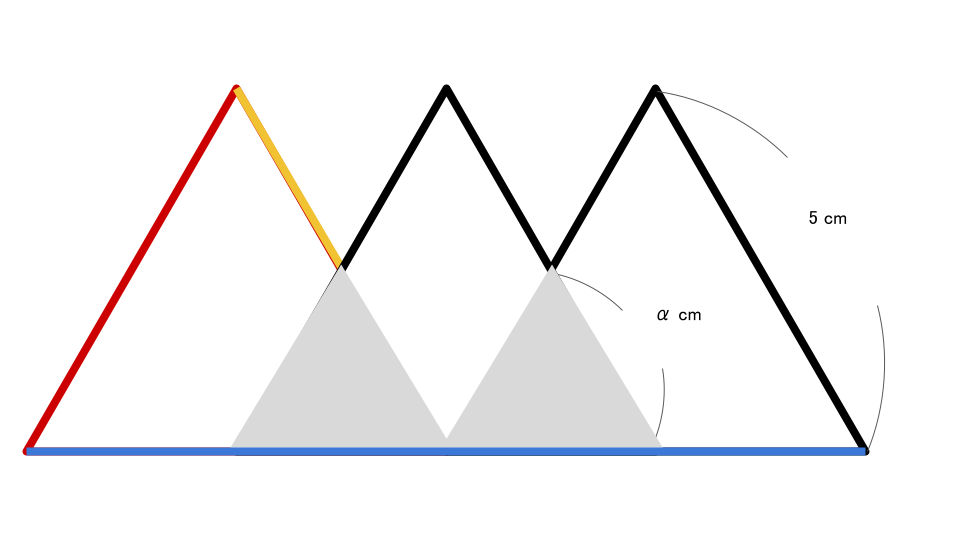
ここで、それぞれの長さを求めてみることにします。
赤色の辺は、問題の条件より \(5cm\) と分かります。
黄色の辺は、大きい三角形の辺から小さい三角形の辺を引いた長さに等しいから、 \((5-a) \ cm\) です。
青色の辺は、大きな三角形の辺3つ分から小さい三角形の辺2つ分を引いた長さに等しいから、 \(5\times 3 -a \times 2=(15-2a) \ cm\) となります。
先ほどの図形の周囲を、3種類の辺で色分けしてみると、赤色の辺が2本、黄色の辺が4本、青色の辺が1本で構成されていることが分かります。
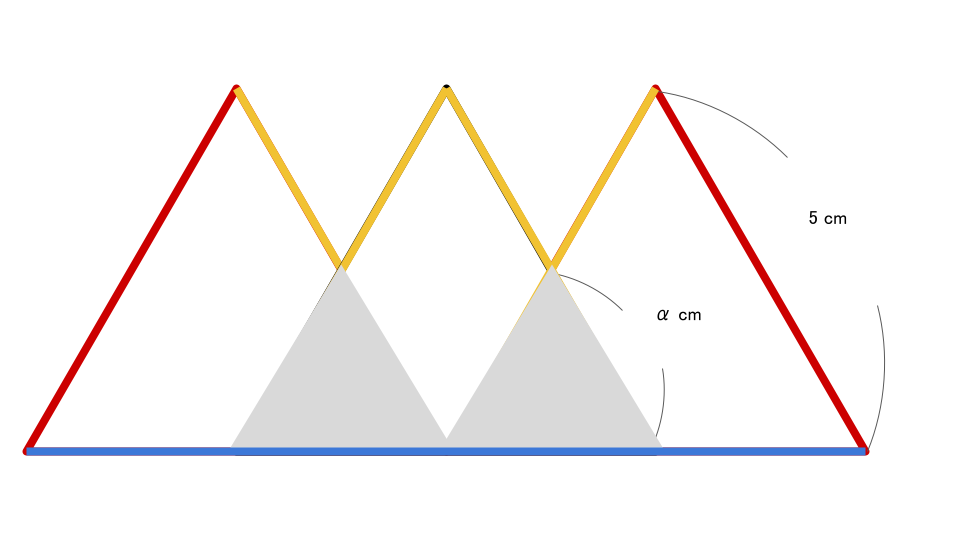
よって、図形の周囲の長さは、
\((赤色の辺)\times 2\) \(+\) \((黄色の辺)\times 4\) \(+\) \((青色の辺)\times 1\)
\(=5 \times 2+(5-a) \times 4+(15-2a)\)
\(=10+20-4a+15-2a\)
\(=45-6a\) となります。
ポイント
・図形の周囲を一気に求めるのではなく、いくつかの長さに分割して考えます
・与えられた値を使って、それぞれの辺の長さを求めます
10
\(n\) は \(100\) より小さい素数である。\(\dfrac{231}{n+2}\) が整数となる \(n\) の値をすべて求めなさい。
答え
\(n=5,\ 19,\ 31\)
解き方
\(\dfrac{231}{n+2}\) が整数となるときを考えます。
これは、分母の \(n+2\) が \(231\) の約数になるときなので、まずは \(231\) の約数を求めてみることにします。
\(231\) の約数は、\(1,\ 3,\ 7,\ 11,\ 21,\ 33,\ 77,\ 231\) の8通りと分かるので、\(n+2=1,\ 3,\ 7,\ 11,\ 21,\ 33,\ 77,\ 231\) が成り立ちます。
これより、\(n=-1,\ 1,\ 5,\ 9,\ 19,\ 31,\ 75,\ 229\) 。
この中で \(100\) より小さい素数は、\(5,\ 19,\ 31\) の3つです。
ポイント
・問題文の条件を注意深く読みます
・\(n\) を求める前に、\(n+2\) がどんな値をとるか考えます
・\(n\) の条件(100未満の素数)に気を付けて、最後の答えを求めます
11
下の図のように,正方形ABCD,正方形EFCGがある。正方形ABCDを,点Cを中心として,時計まわりに \(45^{\circ}\) だけ回転移動させると,正方形EFCGに重ね合わせることができる。このとき,\(\angle x\) の大きさを求めなさい。【一部改題】
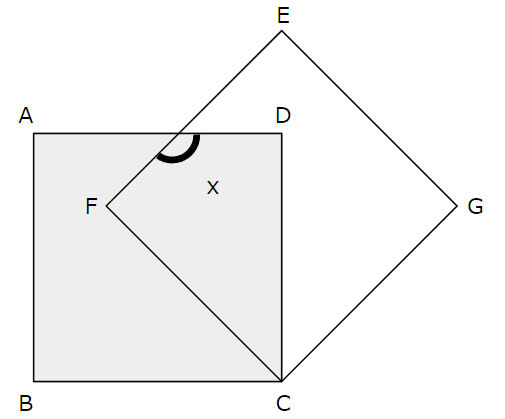
答え
\(135^{\circ}\)
解き方
正方形EFCGは、正方形ABCDを,点Cを中心に \(45^{\circ}\) 回転移動させると重なるから、\(\angle\)BCF は \(45^{\circ}\) と分かります。
また、\(\angle\)BCDは直角で、\(\angle\)BCD\(=\angle\)BCF\(+\angle\)FDC だから、
\(\angle\)FCD\(=\angle\)BCD\(-\angle\)BCF\(=90^{\circ}-45^{\circ}=45^{\circ}\)
次に、\(\angle x\) がある頂点をHとおいて、四角形CDHFに着目します。
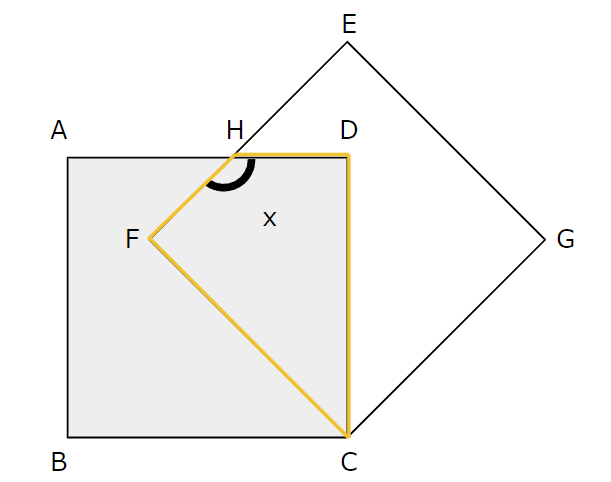
四角形の内角の和は \(360^{\circ}\) であり、\(\angle\)CDHと\(\angle\)HFCは直角で、\(\angle\)FCD\(=45^{\circ}\)だから、
\(\angle\)DHF\(=360^{\circ}-\angle\)FCD\(-\angle\)CDH\(-\angle\)HFC\(=360^{\circ}-45^{\circ}-90^{\circ}-90^{\circ}=135^{\circ}\)
よって、\(\angle x=135^{\circ}\)
ポイント
・角度の分かっている角に注目します
・三角形や四角形の内角の和を利用します
12
下の図で,6点 A,B,C,D,E,Fは,円Oの周上の点であり,線分AEと線分BFは円Oの直径である。点C,点Dは弧BEを3等分する点である。\(\angle\)AOB\(=42^{\circ}\)のとき,\(\angle x\) の大きさを求めなさい。【一部改題】
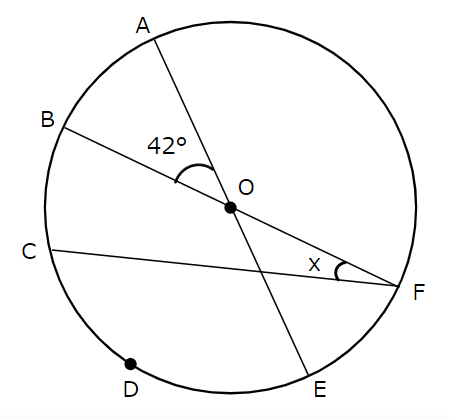
答え
\(\angle x = 23^{\circ}\)
解き方
\(\angle\)AOB\(=42^{\circ}\) で、\(\angle\)AOB\(+ \angle\)EOB\(=180^{\circ}\) だから、
\(\angle\)EOB\(=180^{\circ}- \angle\)AOB\(=180^{\circ}-42^{\circ}=138^{\circ}\)。
点C,点Dは弧BEを3等分する点だから、弧BC\(=\)弧CD\(=\)DEが成り立っています。
ある円において、同じ長さの弧に対する中心角は等しいので、
\(\angle\)BOC\(=\angle\)COD\(=\angle\)DOE
ここで、\(\angle\)EOB\(=\angle\)BOC\(+\angle\)COD\(+\angle\)DOE であることを踏まえると、
\(\angle\)EOB\(=\angle\)BOC\(+\angle\)BOC\(+\angle\)BOC\(=3 \angle\)BOC
と分かります。
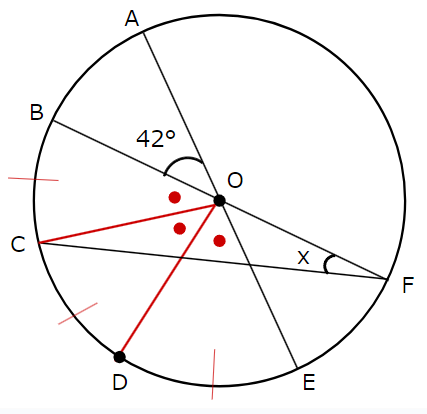
先ほど求めた \(\angle\)EOB\(=138^{\circ}\) より、次の方程式が成り立ちます。
\(3\angle\)BOC \(= \angle\)EOB
\(3 \angle\)BOC \(=138^{\circ}\)
両辺を3で割って、
\(\angle\)BOC \(=46^{\circ}\)
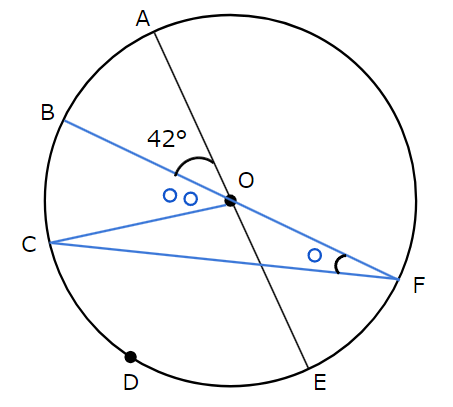
ここから、いよいよ \(\angle x\) 、すなわち \(\angle\)BFC の値を求めていきます。
弧BCに注目して、円周角の定理を用います。
ある弧に対する円周角の大きさは中心角の半分になることと、先ほど求めた \(\angle\)BOC \(=46^{\circ}\) を使って、
\(\angle\)BFC\(=\angle\)BOC \(\div 2=46^{\circ} \div 2=23^{\circ}\)
ポイント
・弧と円周角や中心角の関係性を利用します
・図形に補助線を引いて、同じ角度の角を作ります
13
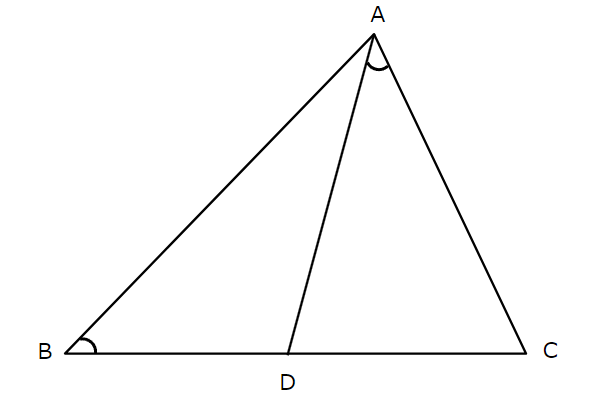
下の図のように,△ABCがあり,点Dは辺BC上にある。AB \(=12cm\),AC \(=8cm\),CD \(=6cm\),\(\angle\)ABC=\(\angle\)DACのとき,線分ADの長さを求めなさい。【一部改題】
答え
AD \(=9cm\)
解き方
△ABCと△DACにおいて、
条件より、\(\angle\)ABC=\(\angle\)DAC \(\cdots ①\)
また、\(\angle\)C は共通だから、\(\angle\)BCA=\(\angle\)ACD \(\cdots ②\)
①と②より、2組の角がそれぞれ等しいので、△ABC \(\backsim\) △DAC
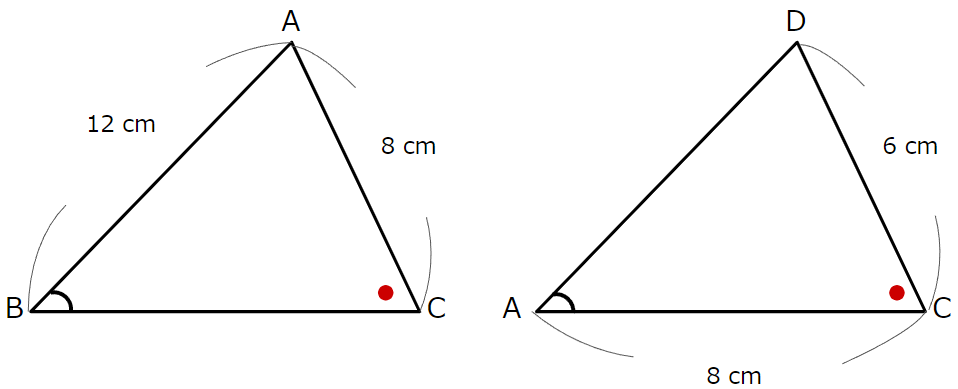
2つの三角形の分かっている辺の長さを書き込むと、上の図のようになります。
相似な図形において、対応する辺の比はそれぞれ等しいから
BA : AD \(=\) AC : DC
\(12\) : AD \(=8\) : \(6\)
\(8\)AD \(=6 \times 12\)
\(8\)AD \(=72\)
これを解くと、AD \(=9cm\) と分かります。
ポイント
・相似な三角形を見つけます
・相似な三角形では、対応する辺の比や角が等しいことを利用します
14
図1のように,三角柱ABC-DEFの形をした透明な容器に,水を入れて密閉した。この容器の側面はすべて長方形で,AB \(=6cm\),BC \(=8cm\),CF \(=12cm\),\(\angle\)ABC \(=90^{\circ}\) である。この容器を,△DEFが容器の底になるように,水平な台の上に置いた。このとき,容器の底から水面までの高さは \(8cm\) である。この容器を図2のように,四角形FEBCが容器の底になるように,水平な台の上に置きかえたとき,容器の底から水面までの高さを求めなさい。ただし,容器の厚みは考えないものとする。
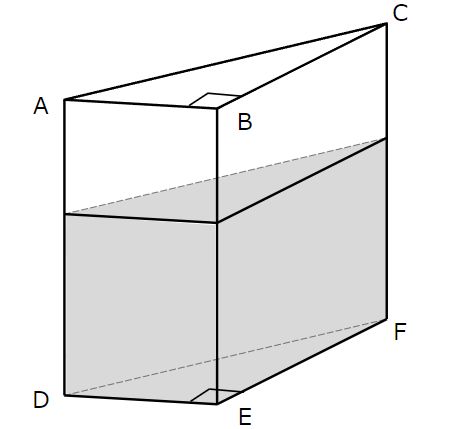
図1
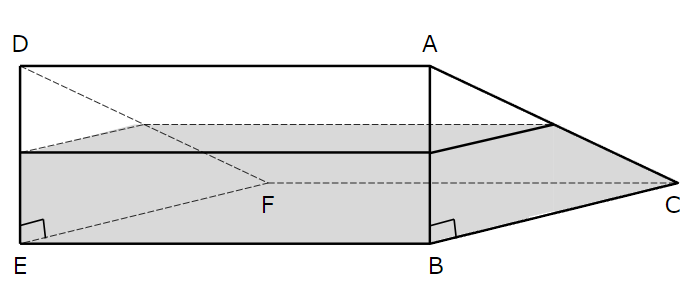
図2
答え
\(=6-2\sqrt{3} \ (cm)\)
解き方
水の入っていない部分の体積から考えていきます。
図1において、CF \(=12cm\) 、容器の底から水面なでの高さは \(8cm\) だから、水が入っていない部分の高さは \(12-8=4 \ (cm)\) と分かります。
ここで、水が入っていない部分は三角柱だから、その体積は 底面積 \(\times\) 高さ で求めることができます。
(△ABCの面積)\(\times 4=(6 \times 8 \div 2)\times 4=96 \ (cm^{3})\)
今度は図2に注目してみましょう。
図2の水が入っていない部分。これは、図1の水の入っていない部分の体積と同じですね。
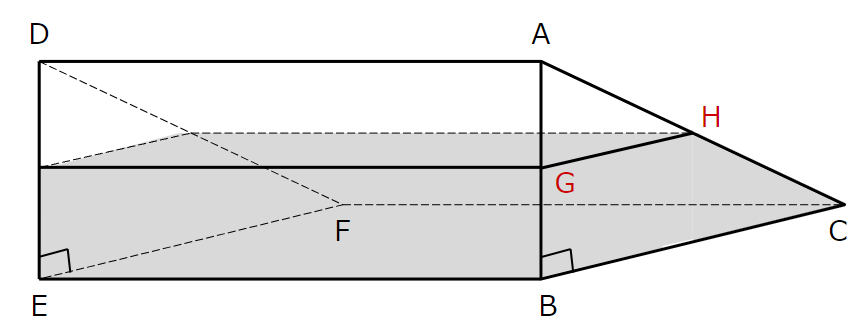
上の図のようにGとHを書き加えると、水が入っていない部分は、底辺が△AGH、高さがADの三角柱と見ることができます。
底辺の三角形の面積を \(x cm^{2}\) とおくと、体積は
\(x \times\) AD\(=96\) 【底面積 \(\times\) 高さ \(=\) 体積】
ADはCFに等しく、長さは \(12cm\) だから
\(x \times 12 =96\)
これを解くと \(x=8\) 。
つまり、△AGHの面積は \(8 cm^{2}\) であることが分かりました。
次に、△AGHと△ABCに着目しましょう。
容器は水平な台の上に置かれているので、水面は底面と平行になっているはずです。
よって、GH // BC が成り立ちます。
平行な線分において、同位角は等しいから、
\(\angle\)AHG=\(\angle\)ACB \(\cdots ①\)
また、角Aは共通だから、
\(\angle\)HAG=\(\angle\)CAB \(\cdots ②\)
①と②より、2組の角がそれぞれ等しいから、△AGH \(\backsim\) △ABC
相似な図形において、面積比は相似比の2乗に等しいという性質を使って、
△AGH : △ABC \(=\) AG\(^{2}\) : AB\(^{2}\)
△AGH\(=8\)、△ABC\(=24\)、AB\(=6\) を上の式にそれぞれ代入して、
\(8:24 =\)AG\(^{2}\) : \(6^{2}\)
\(24 \times \) AG\(^{2}\) \(=8 \times 6^{2}\)
AG\(^{2}\) \(=8 \times 36 \div 24\)
AG\(^{2}\) \(=12\)
AGは辺の長さであり、正の数なので
AG\(=\sqrt{12}=2\sqrt{3}\)
最終的に求めたいのは、図2の状態のときの水が入った部分の高さ、つまりGBです。
GB=AB-AGであり、AB\(=6\)、AG\(=2\sqrt{3}\) なので、
GB\(=6-2\sqrt{3}\)
ポイント
・水が入っていない部分の体積に注目します
・相似な図形の面積比と相似比の関係性を利用して、辺の長さを求めます
15
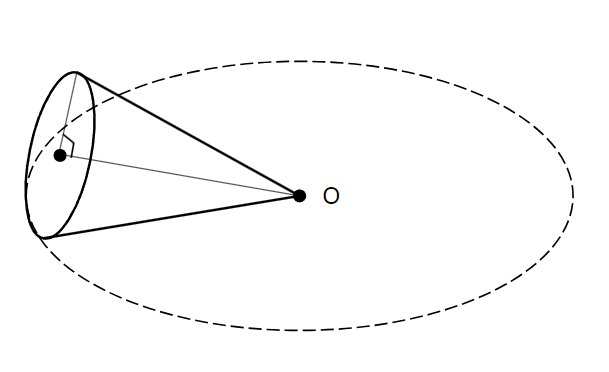
下の図のように,底面の半径が \(4cm\) の円錐を平面上に置き頂点Oを中心としてすべらないように転がした。このとき,点線で表した円Oの上を1周し,もとの場所にもどるまでに3回半だけ回転した。この円錐の表面積を求めなさい。ただし,円周率を \(\pi\) とする。【一部改題】
答え
\(72 \pi cm^{2}\)
解き方
まずは、円Oの円周を求めます。
問題文から、円Oの円周は 半径 \(4cm\) の円錐の底辺の円の円周 \(3.5\) 個分に等しいことが分かります。
円錐の底辺の円周は、円周を求める公式 \(2 \times 半径 \times \pi\) にあてはめて計算すると、
\(2 \times 4 \times \pi = 8 \pi\) となります。
よって、円Oの円周は
\(8 \pi \times 3.5=28 \pi cm\) と分かります。
次に、円Oの半径を求めます。
これも先ほどの公式を利用すると
\(2 \times\) (円Oの半径) \(\times \pi = 28 \pi\)
両辺を \(2 \pi\) で割って、円Oの半径は \(14cm\) と出すことができました。
あとは、円錐の表面積を求めればよいですね。
円錐の表面積は 底面積 \(+\) 側面積 で値を出せるので、それぞれの面積を求めてみます。
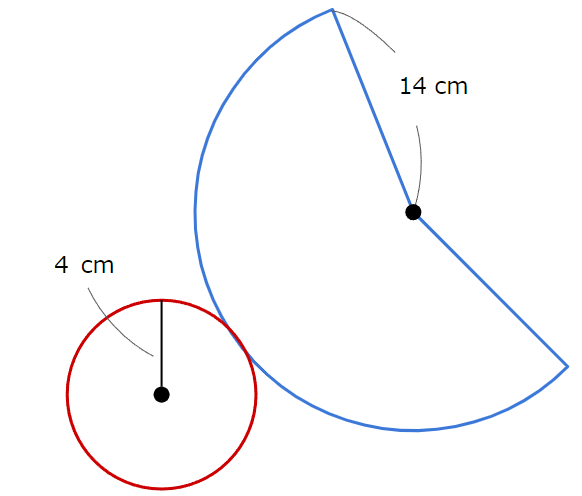
まずは、底面積です。
円錐の底面は半径 \(4cm\) の円なので、その面積は
\(4 \times 4 \times \pi = 16 \pi cm^{2}\)
次に、側面積を求めます。
円錐の側面積は、底面の円の半径に母線の長さ(この問題では、円Oの半径に等しいです)と\(\pi\)をかけた値になるので、
\(4 \times 14 \times \pi = 56 \pi \ (cm^{2})\)
したがって、円錐の表面積は
底面積 \(+\) 側面積
\(=\)\(16 \pi \) \(+\) \(56 \pi \) \(=72 \pi \ (cm^{2})\)
ポイント
・図形の面積や立体の表面積の公式を押さえておきます
・特に、円錐の側面積の求め方は頻出です


