中学数学で学ぶ計算の用語
中学数学では今まで習ってきた足し算などを別の言い方で表します。ここではその用語について紹介します。
これらのようにそれぞれの計算の種類を表します。次にこれらの計算の答えの表し方についてみてみましょう。
このように中学数学では漢字１文字で表します。ここでは加法と減法についてを説明していきたいと思います。
加法
正の数と正の数、正の数と負の数、負の数と負の数の組に分けることができます。
まず正の数と正の数についてですがこれは小学校で解いていた
\(1+2=3\)
のような計算とおなじです。
次に正の数と負の数の加法についてです。式の例はこのような形です。
\(3+(-2)=1\)
のようになります。負の数を加法を使って表す際にはかっこで負の数を挟みます。また、この計算をするとき数直線をイメージすると考えやすいです。
―数直線について忘れてしまったひとはこちら（練習問題付き）
例で挙げた式で試してみましょう。3にー2（０よりも２小さい数）を足すと考えてみましょう。そうすると答えは３よりも２小さい数１になります。
今の説明を見てもよくわからないという人もお金の計算を考えるとわかりやすいと思います。
A君は３円もっています。そして、Bくんに２円の借金をしています。この時にAくんが借金を返すと所持金は何円になりますか？
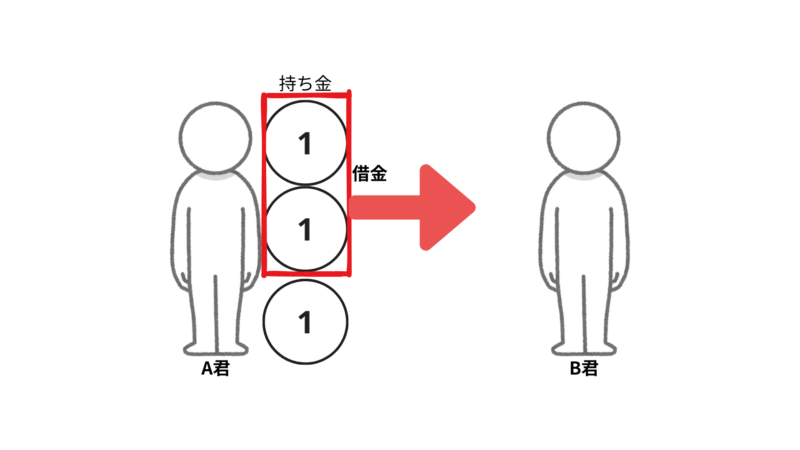
B君に借金を返して残った１円がA君の所持金です。
これをさっきあげた式と比べてみましょう。
ー２を借金と考えることで理解しやすいと思います。
そしてこの計算をして気づいた人もいると思いますが加法をする際の＋（ー２）という部分はー２に変えることができます。
\(3+(-2)=3-2\)
符号について慣れてきたらこれを変換してから計算するとより早くなると思います。
そして負の数と負の数についてです。式の例は
\(-3+(-2)=-5\)
のようになります。ー３にー２（０より２小さい数）を足すと考えると答えは５になります。
また、お金の計算を利用すると、
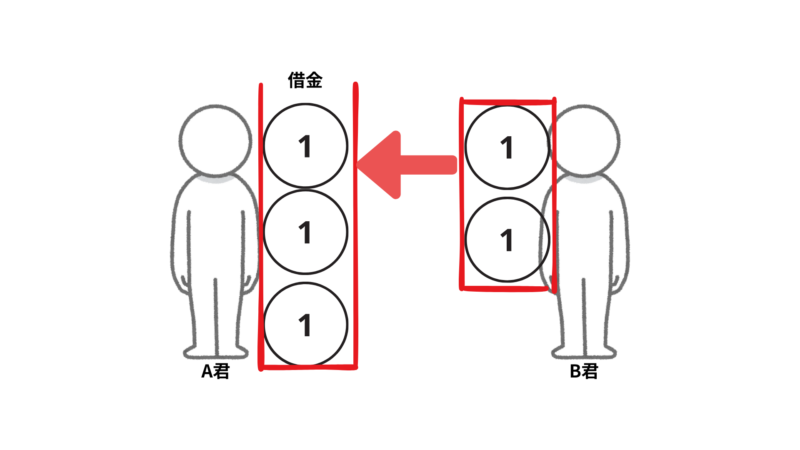
３円の借金をA君がしていてさらにB君から２円借金したら借金の合計は５円です。このように正の数と負の数との組み合わせのものと同じように考えて計算できます。
この組み合わせは引かれる数が負の数になっているのがほかの組み合わせと違うポイントです。
加法で利用できる法則
加法では交換法則と結合法則という2つの法則が成り立ちます。
交換法則
交換法則とは順序を入れ替えて足し算をしても変わらないという法則です。言葉だけでは難しいので式を見て説明します。
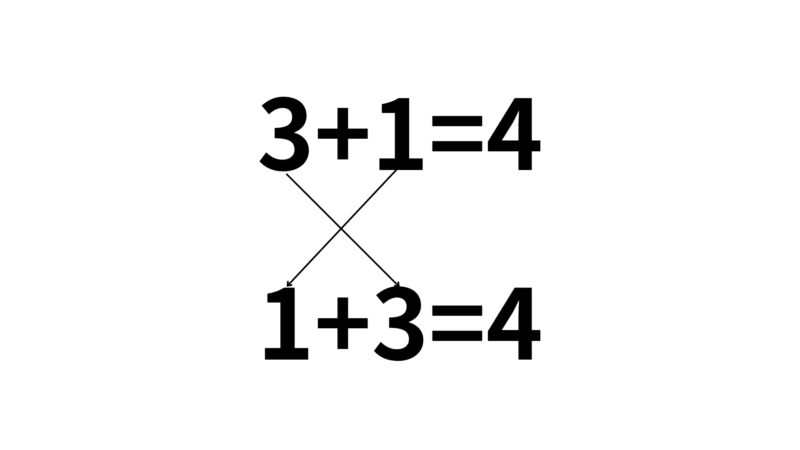
この上の式は３と１を入れ替えた２つの式です。計算してみるとどちらも４になると思います。このように加法の場合足す順番を変化させても答えは変わりません。
結合法則
結合法則とはかっこをどこに付けても答えが変わらないという法則です。
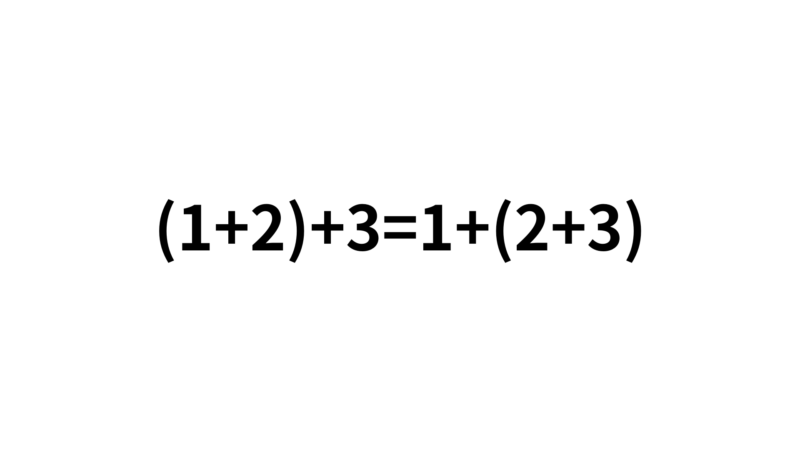
左辺は１＋２に右辺は２＋３にかっこがついてますが、どちらも答えは６でかっこの位置を変化させても答えは変わりません。これが交換法則です。
減法
減法も加法と同様にして正の数と正の数、正の数と負の数、負の数と負の数の組に分けることができます。
まず正の数と正の数の減法をみていきましょう。
\(6-3=3\)
のように引く数が引かれる数より小さければ小学校で学んだ計算と同じです。しかし、
\(2-3=-1\)
のように引く数のほうが大きい場合答えが負の数になります。
次に正の数と負の数の組み合わせをみてみます。
\(2-(-4)=6\)
このような式になり加法と同じように（）で負の数を囲みます。そして引く数が負の数の場合は―（負の数）→＋（正の数）にすることができます。
例 \(5-(-3)=5+3\)
このように変形し加法の計算に変えることができます。
最後に負の数と負の数の組み合わせです。
\(-4-(-6)=2\)
このような式になり、先ほど正の数と負の数との組み合わせの時と同じように加法に変換すると
\(-4+6=2\)
となり加法として計算できます。
では演習問題を解いて練習しましょう。計算問題は練習あるのみです。
演習
問題を解いて、ここまでの内容を復習してみましょう。
